Решить, ! 1. автомобиль массой 3 т движется вверх по наклонной плоскости с постоянной скоростью v =10 м/с. угол наклонной плоскости 30, коэффициент трения μ = 0,02. найти силу тяги автомобиля. 2. однородный стержень длиной l = 1,2 м и массой m = 0,3 кг вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через один из его концов с угловым ускорением = 9,81 с-1. сколько оборотов сделает стержень за время t = 5,0 с, если он начал вращаться из состояния покоя? как изменится вращающий момент, если ось вращения переместить в центр масс стержня, а действующая сила не изменяется? 3. шар массой m = 3 кг скатывается без проскальзывания с вершины наклонной плоскости высотой h = 4 м без начальной скорости. длина ската наклонной плоскости l = 8 м, а значение коэффициента трения качения () тела одинаково на всем протяжении его пути и равно =0,1. определите скорость шара у подножия наклонной плоскости (в м/с).
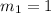 кг
кг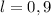 м
м °
° кг
кг м/с
м/с м/с
м/с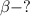
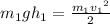
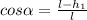
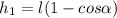
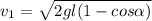
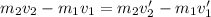 ,
,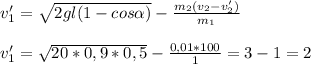

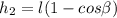
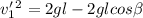
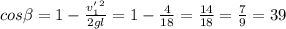 °
°
Заметим, что при прохождении точки π/2 шарик должен иметь неотличимое натяжение нити, иначе она согнется и полный оборот не получится.
Тогда по второму закону Ньютона имеем: mg = ma, т.е. a = g
Центростремительное ускорение шарика в точке π/2: g = V2^2 / R => V2^2 = g R
Теперь прибегнем к закону сохранения энергии (в точке -π/2 и π/2). Получаем (V1 - начальная скорость шарика, которую мы ищем):
mV1^2 / 2 = mV2^2/2 + mg2R
mV1^2 / 2 = (mgR + 4mgR) / 2
mV1^2 = 5mgR
V1 = √5gR