1.Моментом силы относительно точки называется векторное произведение радиус-вектора точки приложения силы на вектор силы
2.Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении
3.Моме́нт и́мпульса (момент импульса относительно точки, также: кинетический момент, угловой момент, орбитальный момент, момент количества движения) — физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение[1].
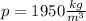
Введение и выражение величин:
Пусть плотность первой жидкости 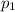 , второй жидкости
, второй жидкости 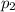 , а шара
, а шара 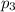 , тогда запишем общий объём шара
, тогда запишем общий объём шара 
Найдем объем шара находящийся над водой, для этого общий объем разделим на 4 (по условию), и получим 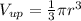 (1)
(1)
Повторим для нижней части шара, только умножим на 3/4, так как логично, что оставшаяся часть шара под разделом жидкостей, и получим 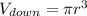 (2)
(2)
Чтобы найти массы этих частей шара, надо найденный объем умножить на плотность шара:
 (3)
(3)
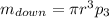 (4)
(4)
Работа с формулами и уравнением:
На шар действуют 2 силы: Архимеда и тяжести, так как шар неподвижен, то сила действующая на обе части "вниз", равна силе действующей на обе части "вверх", запишем общий вид:
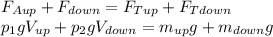
Подставим объем и массы из пунктов (1-4) и сократим на 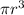 и на
и на  , в итоге останется:
, в итоге останется:
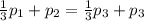
Подставим значения 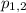 и решим уравнение:
и решим уравнение:
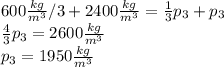
Получим те самые циферки из ответа
Н= H0 + vv/2g = 50+25/20=51.24м
H-h=gtt/2
t=Y2(H-H0)/g
t=Y2*41.24/10=2.87c