ответ:1. Многоуровневый рычаг в целом состоит из трёх рычагов. Для того чтобы вся система находилась в состоянии равновесия, в равновесии должен находиться каждый отдельный рычаг.
На рисунке внизу видно, что всего имеется шесть плечей силы. Значения их длин необходимо определить по рисунку, приведённому в задании:
l1=2,l2=1,l3=1,l4=3,L1=4,L2=2.
2. Прежде всего имеется возможность определить массу противовеса m2, при которой верхний левый рычаг будет находиться в равновесии. Для этого необходимо использовать условие равновесия рычага: F1⋅l1=F2⋅l2.
Так как сила тяжести, создаваемая противовесом, пропорциональна его массе, то вместо силы тяжести можно использовать массу, получив таким образом:
m2=m1⋅l1l2=32⋅21=64кг.
3. Для того чтобы нижний рычаг находился в состоянии равновесия, необходимо выполнение условия: (m1+m2)⋅L1=(m3+m4)⋅L2, что позволяет узнать общую массу 3-го и 4-го противовеса:
(m3+m4)=(m1+m2)⋅L1L2=(32+64)⋅42=192кг.
4. Чтобы верхний правый рычаг находился в состоянии равновесия, общая масса m3+m4 должна распределяться обратно пропорционально плечам силы рычага, то есть:
m3m4=l4l3=31.
Таким образом получаем систему уравнений:
{m3+m4=192m3=31⋅m4
Подставляя в первое уравнение выражение для m3, из второго уравнения получаем:
31⋅m4+m4=(3+1)⋅m4=192.
После выполнения преобразований получаем:
m4=192(3+1)=48кг.
5. m3 определяют из выражения для общей массы правого верхнего рычага m3=192−m4=192−48=144кг.
Рычаг находится в равновесии, если массы противовесов равны:
m2=64кг,
m3=144кг,
m4=48кг.
Объяснение:
Объяснение:
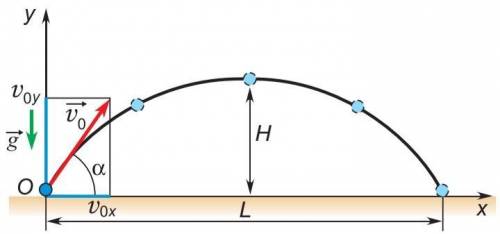
1) форму параболы ( с вершиной параболы в высшей точке траектории )
2) В начале движения тела с начальной скоростью ( v0 ) проекция которой на ось Ох ( v0x ) равна ( v0cosα ) , a на ось Оу ( v0y ) равна ( v0sinα )
В высшей точки траектории vy = 0 м/с
Поэтому
0 = v0sinα - gt
отсюда
tп. ( время подъема ) = t = ( v0sinα ) / g
Дальность полёта тела будет вычисляться как
L = vxtпол.
Где tпол. ( полное время движения ) = 2tп. = ( 2v0sinα ) / g
L = ( v0cosα2v0sinα ) / g
2sinαcosα = sin2α , поэтому
L = ( v0²sin2α ) / g
Но sin90° = 1 , поэтому если α = 45° , то sin2α = 1
Поэтому именно при угле бросания равным 45° будет максимальная дальность полета
3) В наивысшей точке траектории скорость тела сонаправлена с осью горизонта , поэтому угол между горизонтом и вектором скорости тела в данный момент времени равен 0°
Так как траекторией движения тела брошенного под углом является парабола тогда в конечной точке траектории угол между горизонтом и вектором направления направления скорости будет равен углу между вектором начальным скорости и горизонтом .
S=V0^2/2*a
a=k*m*g/m=k*g
S=V0^2/2*k*g
V0=sqrt(2*k*g*S)=sqrt(2*0,8*10*25)=20 м/с