Объяснение:
α = β
Не удивительно, что это запомнилось?
5 законов физики, которые остаются в памяти на всю жизнь
Закон АрхимедаНа тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела. Помните? Мне почему-то больше вспоминается мультик «Коля, Оля и Архимед». Хорошие были познавательные мультики в СССР. Ну а формула выглядит так:
FА = ρжgVпт,
где FА - сила Архимеда;
ρж – плотность жидкости;
Vпт – объем погруженной в жидкость части тела.
Хотя для большинства школьников более памятно:
По закону Архимеда после сытного обеда полагается поспать!
Сила тока и напряжение
А вот и знаменитый закон Ома! Сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника. Формула выглядит так:
I=U/R,
где:
I – сила тока в проводнике, единица измерения силы тока (ампер);
U – электрическое напряжение (разность потенциалов), единица измерения напряжения (вольт);
R – электрическое сопротивление проводника, единица измерения электрического сопротивления (Ом).
И это главный закон всех электриков. Учитель физики об этом говорил, и именно этим мне этот закон и запомнился.
5 законов физики, которые остаются в памяти на всю жизнь
Когда нужно немного тепла
Сразу же вспоминается еще один «электрический» закон Джоуля-Ленца. Русский физик Э. Ленц и английский физик Д. Джоуль независимо друг от друга, но почти одновременно (в 1841 и 1842 году) совершили открытие, что:
При прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику.
Кстати обидно, что то самое количество теплоты, создаваемое током, стали измерять в джоулях и обозначать буквой Q (Дж). Почему не в ленцах? Видимо потому, что английский ученый все же был первым. А формула выглядит так:
Q = ∫ k • I² • R • t,
где:
Q – количество выделившейся теплоты;
I – величина тока;
R — активное сопротивление проводников;
t – время воздействия;
k – тепловой эквивалент работы.
Коэффициент полезного действия
Ну и пятый физический закон, который годы не смогли вытеснить из моей памяти, это один из важных законов механики, который звучит так:
Коэффициент полезного действия представляет собой отношение отдаваемой мощности к подводимой мощности.
То есть, отношение полезной работы, совершенной механизмом, ко всей затраченной работе (подведенной энергии) за то же время. Видимо мне очень понравилась аббревиатура КПД (нравится до сих пор), а возможно, то, что можно посчитать производительность. Сказать сложно, но даже формулу помню наизусть:
5 законов физики, которые остаются в памяти на всю жизнь
А про Ньютона то чуть не забыли!
Кстати, я совсем забыла о трех законах Ньютона. И закон про силу притяжения. Их я тоже помню, так что пусть они будут вне этого ТОПа, бонусом. И о них я узнала тоже раньше, чем начала изучать физику в школе. Конечно же, из мультика.
 – длина одного вагона или локомотива,
– длина одного вагона или локомотива,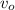 – скорость передней точки локомотива, когда он проезжает мимо,
– скорость передней точки локомотива, когда он проезжает мимо,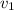 – скорость поезда, когда локомотив только что проехал наблюдателя,
– скорость поезда, когда локомотив только что проехал наблюдателя, – скорость поезда, когда только k вагонов ещё не проехали мимо,
– скорость поезда, когда только k вагонов ещё не проехали мимо, – скорость поезда, когда весь поезд проехал наблюдателя,
– скорость поезда, когда весь поезд проехал наблюдателя,
 наступило состояние
наступило состояние 
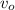 и
и  – отделаят промежуток времени
– отделаят промежуток времени 
 и
и  – очевидно отделаят промежуток времени
– очевидно отделаят промежуток времени 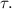
 [1]
[1]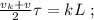 [2]
[2]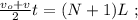 [3]
[3]
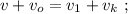 [4]
[4]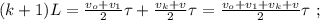
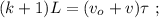
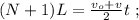
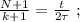
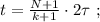 [5] – это всё время движения поезда мимо наблюдателя:
[5] – это всё время движения поезда мимо наблюдателя: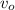 до значения
до значения 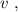 изменяясь на величину
изменяясь на величину 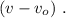
 скорость возрастёт только на величину:
скорость возрастёт только на величину: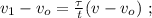
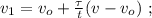

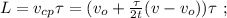 [6]
[6]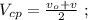
 [7]
[7]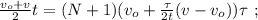
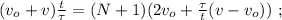
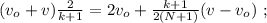


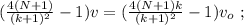
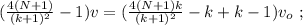


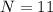 и
и 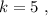 получаем:
получаем: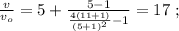
 и
и 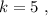 получаем:
получаем: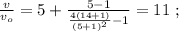
 и
и 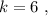 получаем:
получаем: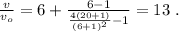
n=P/k*T=1,5*10^6/1,38*10^-23*723=1,5*10^26 1/м3