№1. а) сила Архимеда одинакова (она определяется объемом погруженного в жидкость тела); б) так как плотность меди больше плотности алюминия, объем медного шара равной массы будет меньше, соответственно сила Архимеда, действующая на него будет меньше.
№2. С гидростатического взвешивания измеряют плотности твердых тел и жидкостей. В первом случае твердое тело взвешивают в воздухе и в жидкости, определяя массу и объем, соответственно, а потом деля одно на другое. Во втором - берут тело известной массы и объема, взвешивают его в жидкости, определяя силу Архимеда, а затем плотность жидкости.
№3. Если взять плотность гранита 2600 кг/м^3, то объем камня равен 0.0038 м^3, а сила Архимеда, действующая на него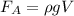 
= 38 Н (
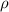= 1000 кг/м^3 - плотность воды). Вычитая из силы тяжести (mg=10 кг*9.8 м/с^2 = 98 Н) силу Архимеда получим силу, которую надо приложить, чтобы поднять камень, 60 Н.
Объяснение:1) Погрешность определения длины стороны кубика будет наименьшей в третьем случае, так как используемое количество кубиков сахара в этом случае больше.
2) Из первого эксперимента можно сделать вывод, что размер одного кубика меньше, чем 10/7 см, но больше, чем 10/8 см.
Из второго опыта следует, что размер кубика меньше, чем 20/40 см = 10/7 см и больше, чем 20/15 см = 4/3 см.
Из третьего опыта — что размер кубика меньше чем 30/22 см = 15/11 см и больше, чем 30/23 см.
3) Из всех опытов можно сделать вывод, что размер кубика лежит в пределах от 4/3 см до 15/11 см, или, что то же самое, от 88/66 см до 90/66 см.
Таким образом, можно сказать, что размер стороны кубика лежит посередине между этими величинами, то есть d = (89/66 ± 1/66) см.
Переводя в десятичную дробь, запишем: d = (1,35 ± 0,02) см.
1) В третьем случае, так как используемое количество кубиков сахара больше.
2) 10/8 см < d < 10/7 см; 4/3 см < d < 10/7 см; 30/23 см < d < 15/11 см.
3) d = (1,35 ± 0,02) см.
