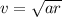, где a - модуль вектора центростремительного ускорения тела, видно, что скорость прямо пропорциональна расстоянию от центра окружности, по которой движется тело (каждая точка будет двигаться тем быстрее, чем дальше она находится от центра вращения), поэтому на корабле качка будет усиливаться по мере приближения к носу.
ответ:
объяснение:
на основании закона сохранения и превращения энергии составим уравнение:
wк1+wp1=wk2+wp2, где wк1, wp1 -кинетическая и потенциальная энергия шарика, находящегося на высоте h на наклонной плоскости; wк2, wp2 - кинетическая и потенциальная энергия шарика у основания наклонной плоскости.
нулевой уровень потенциальной энергии совместим с основанием наклонной плоскости. тогда
wp1 = mgh+q1*q2/4*pi*e0*h
wk1 = 0
второе слагаемое в выражении для wpl представляет собой потенциальную энергию, обусловленную взаимным расположением зарядов q1 и q2. пусть υ — скорость шарика у основания наклонной плоскости. тогда
wk2=m*v^2/2.
в это время расстояние между , как видно из рисунка, равно h/tgα. поэтому
wp2 = q1*q2*tga/4*pi*e0*h
с учетом этих значений энергии уравнение первое примет вид:
mgh+q1*q2/4*pi*e0*h = m*v^2/2 + q1*q2*tga/4*pi*e0*h
отсюда найдем скорость:
v = √2h+q1*q2*tga/2*pi*m*e0*h(1-tga)
