Моделируем камень точечной массой (точкой). Введём систему координат на плоскости с центром в точке-камне перед моментом броска. Ось y направлена вертикально вверх, ось x — ортогональна y в плоскости движения. Моменту броска присвоим время t=0.
Запишем ускорения точки (движение в поле силы тяжести):
Интегрируя, получим:
Начальные условия:
Отсюда:
Найдём экстремумы для , приравняв :
Поскольку , то полученный экстемум является максимумом для .
Наибольшая координата y, достигаемая при моменте времени t*, и будет искомой высотой:
Водород, заполняющий шарик, находится под давлением, немного превышающим атмосферное, за счет силы упругости шарика. При подъеме в более разреженные слои атмосферы (на каждые 100 м подъема давление падает примерно на 10 мм рт. ст. или на 1333 Па) внутреннее давление водорода в шарике перестает уравновешиваться атмосферным и шарик увеличивается в объеме до тех пор, пока понижение внешнего давления не компенсируется возрастающей силой упругости шарика. Разумеется, до бесконечности это продолжаться не может..)) Рано или поздно прочности шарика не хватит и он лопнет. Именно поэтому при запуске метеозондов на большую высоту (порядка 10 км - 217 мм рт.ст) заполняют гелием или водородом примерно на треть.
Водород, заполняющий шарик, находится под давлением, немного превышающим атмосферное, за счет силы упругости шарика. При подъеме в более разреженные слои атмосферы (на каждые 100 м подъема давление падает примерно на 10 мм рт. ст. или на 1333 Па) внутреннее давление водорода в шарике перестает уравновешиваться атмосферным и шарик увеличивается в объеме до тех пор, пока понижение внешнего давления не компенсируется возрастающей силой упругости шарика. Разумеется, до бесконечности это продолжаться не может..)) Рано или поздно прочности шарика не хватит и он лопнет. Именно поэтому при запуске метеозондов на большую высоту (порядка 10 км - 217 мм рт.ст) заполняют гелием или водородом примерно на треть.
Моделируем камень точечной массой (точкой). Введём систему координат на плоскости с центром в точке-камне перед моментом броска. Ось y направлена вертикально вверх, ось x — ортогональна y в плоскости движения. Моменту броска присвоим время t=0.
Запишем ускорения точки (движение в поле силы тяжести):
Интегрируя, получим:
Начальные условия:
Отсюда:
Найдём экстремумы для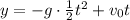 , приравняв
, приравняв 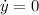 :
:
Поскольку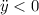 , то полученный экстемум является максимумом для
, то полученный экстемум является максимумом для 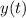 .
.
Наибольшая координата y, достигаемая при моменте времени t*, и будет искомой высотой:
Принимая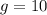 м/с² и имея по условию
м/с² и имея по условию 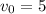 м/с, получим:
м/с, получим:
ответ: 1,25 м.