Однордный стержень длиной 1.2 м лежит на упоре . для удержания стержня в горизонтальном положении нужно давить с силой на её короткий конец f1= 200h , либо действовать с направленной вертикально вверх силой f2= 100 h на ее длинный конец. определите массу и ее расположение точки упора
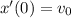 .
.
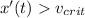 .
.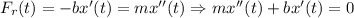
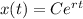 . Тогда дифференциальное уравнение имеет вид
. Тогда дифференциальное уравнение имеет вид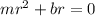
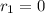
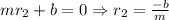
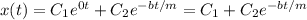
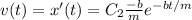
 ,
, 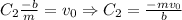 .
.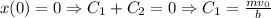
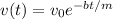
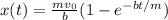
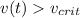 , то есть
, то есть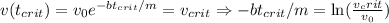
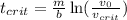
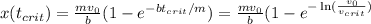
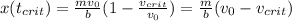
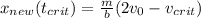
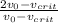 ,
,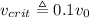 , это отношение равно
, это отношение равно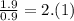 .
.