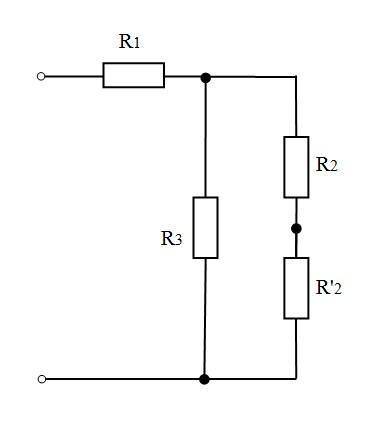
Схема состоит из:
группы сопротивлений R₂ и R₂', соединенных последовательно,
сопротивления R₃, соединенного параллельно с первой группой,
сопротивления R₁, соединенного последовательно с первыми двумя группами.
Преобразовать схему можно так: (см. рис.1)
Тогда общее сопротивление R₂ и R₂':
R₂₂ = R₂ + R₂' = 20 + 20 = 40 (Ом)
То есть сопротивления R₂ и R₂' можно заменить одним сопротивлением R₂₂ = 40 (Ом) (см. рис.2)
Общее сопротивление R₂₂ и R₃:
R₂₂₃ = R₂₂•R₃ : (R₂₂+R₃) = 40•60 : 100 = 24 (Ом)
Общее сопротивление цепи с учетом R₁:
R = R₁ + R₂₂₃ = 6 + 24 = 30 (Ом)
Общий ток в цепи:
I = I₁ = U/R = 240 : 30 = 8 (A)
Напряжение на первом сопротивлении:
U₁ = I · R₁ = 8 · 6 = 48 (B)
Напряжение на группе сопротивлений R₂₂₃:
U₂₂₃ = U - U₁ = 240 - 48 = 192 (B)
Ток, протекающий через R₃:
I₃ = U₂₂₃ : R₃ = 192 : 60 = 3,2 (A)
Ток, протекающий через R₂₂:
I₂₂ = U₂₂₃ : R₂₂ = 192 : 40 = 4,8 (A)
Напряжение на R₂ и R₂':
U₂ = U₂' = R₂I₂₂ = R₂'I₂₂ = 20 · 4,8 = 96 (B)
Условие задачи:
Два тела масс m1 и m2, связанные невесомой нитью, лежат на гладкой горизонтальной поверхности. Нить обрывается, если сила её натяжения превышает значение Tm. C какой максимальной горизонтальной силой F можно тянуть второе тело, чтобы нить не оборвалась?
Задача №2.1.82 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
m1, m2, Tm, Fm−?
Решение задачи:
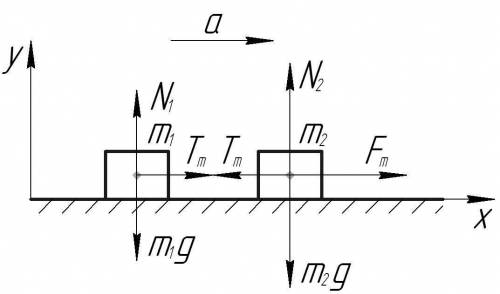
Схема к решению задачиПотянем второе тело с такой силой Fm, что сила натяжения нити, соединяющей тела, станет очень близка по величине к Tm, но ещё не разорвется.
По условию поверхность, по которой движутся тела, гладкая, значит сил трения нет. Покажем на схеме все силы, действующие на тела, потом запишем второй закон Ньютона для обоих тел в проекции на ось x. Ускорения рассматриваемых тел, естественно, одинаковые.
{Fm—Tm=m2aTm=m1a
Сложим оба выражения системы, а из полученного выразим ускорение a.
Fm=(m1+m2)a
a=Fmm1+m2
Подставим формулу в последнее выражение системы, а оттуда выразим искомую силу Fm.
Tm=Fmm1m1+m2
Fm=Tm(m1+m2)m1
Поделим почленно числитель дроби на знаменатель.
Fm=Tm(1+m2m1)
В условии не было дано числовых данных, задачу требовалось решить в общем виде, что мы и сделали.
ответ: Tm(1+m2m1)
Еп=300Н/м*(0,1)^2 м^2/2=1,5 Н*м=1,5 Дж.
Растянутая или сжатая пружина может совершить работу, значит обладает энергией, недеформированная пружина энергией не обладает. (0,4*1/4=0,1м).