ДАНО
L
H
-------------------------
S - ?
РЕШЕНИЕ
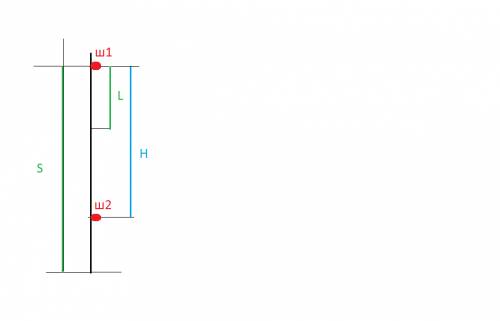
Обозначим S- высота башни
Сразу понятно, что L не равно H .(см на рисунке)
ШАРИК 1
начальная скорость V1o=0
в конце отрезка L имеет скорость V (найдем, нужда для решения)
L=(V^2-V1o^2)/2g=V^2/2g
V=√(2gL) (1)
за остальное время t - шарик 1 пролетел расстояние S-L (с начальной скоростью V)
S- L = Vt +gt^2/2 (2)
ШАРИК 2
начальная скорость V2o=0
S- H высота , с которой началось падение
падение длилось тоже время t
S-H = V2ot +gt^2/2 = gt^2/2 (3)
S-H = gt^2/2
t^2 =2(S-H)/g
t =√(2(S-H)/g ) (4)
подставим (1)(3)и(4) в (2)
S- L = Vt +gt^2/2 = √(2gL) *√(2(S-H)/g ) + (S-H)
S- L- (S-H) = √(2gL) *√(2(S-H)/g)
H-L =√(4L(S-H))
(H-L)^2 =4L(S-H)
S-H=(H-L)^2 /(4L)
S= (H-L)^2 /(4L) + H
ответ высота башни (H-L)^2 /(4L) + H
Q = Q1 + Q2
Q1 = ΔEk = (M/2) * (v^2 - v'^2), где v' - скорость тележки с камнем после столкновения
так как кирпич остается на тележке, то удар абсолютно неупругий
по закону сохранения импульса в проекции на некоторую ось:
M v = (m + M) v' => v' = M v / (m + M)
следовательно, Q1 = (M/2) * (v^2 - (M v / (m + M))^2)
Q2 = ΔEp = mgh (пусть тележка - уровень отсчета потенциальной энергии; пренебрежем сопротивлением воздуха)
Q = (M/2) * (v^2 - (M v / (m + M))^2) + mgh