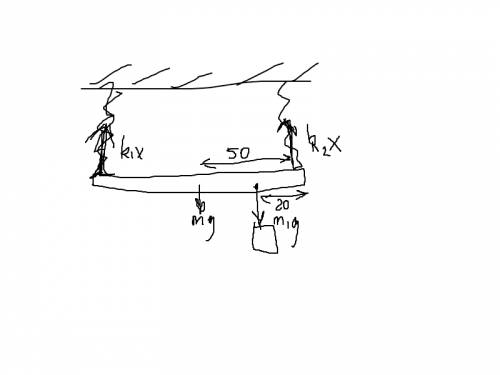
Из закона преломления
Sin α₁ = n Sin β₁ (n - коэффициент преломления)
Sin α₂ = n Sin β₂
Из геометрических вычислений:
180 - φ = 360 - α₁ - α₂ - (180 - γ) ⇒ φ = α₁ + α₂ - γ
γ = β₁ + β₂
С учетом того, что всегда присутствуют аберрации, нужно их минимизировать (между φ и α зависимость нелинейная). т.е. зависимость φ от α должна быть минимальной. Приравняем производную φ к нулю:
dφ = dα₁ + dα₂ ⇒ dα₁ = -dα₂
Дифференцируем остальные уравнения:
dβ₁ + dβ₂ = 0
Cos α₁ dα₁ = n Cos β₁ dβ₁
Cos α₂ dα₂ = n Cos β₂ dβ₂
откуда получим следующее:
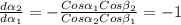
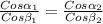
Возводим в квадрат обе части и заменив углы β на α, пользуясь законом преломления, получим:
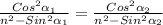
Искомое равенство удовлетворяется при α₁ = α₂, что соответствует минимуму угла φ. Из α₁ = α₂ следует, что β₁ = β₂. Таким образом, падающий и выходящий лучи симметричны по отношению к граням призмы.
Симметричный ход луча соответствует минимуму угла отклонения.
Прилагаю рисунок к ходу мыслей
http://s44.radikal.ru/i103/1207/fa/df6a5763cc0d.jpg
Рассмотрим палку в состоянии равновесия с новым грузом.
Необходимо, чтоб наблюдалось: сумма сил равна 0, и сумма моментов сил тоже равна 0(всё это следует из равновесия системы.)
k1x+k2x=mg+m1g => (k1+k2)x=g(m+m1) векторно сумма сил равна 0.
Выберес осью вращения - место подвеса левой пружины. Тогда: 0.5mg+0.8m1g=1*k2x(это можно понять из рисунка.)
Значит x=g(0.5m+0.8m1)/k2=g(m+m1)/(k1+k2)(из каждого уравнения по равенству)
(0.5m+0.8m1)(k1+k2)=k2(m+m1). k2/(k1+k2)=2/3.(из жесткостей пружин)
0.5m+0.8m1=m2/3+m1*2/3;
m1(4/5-2/3)=m(2/3-1/2);
m1=m(1/6)/(2/15)=m15/12=m1.25=2.5кг.
ответ: 2.5 кг(если я где-то в математике не ошибся =) )