Если шарик сплошной, то его плотность должна быть равна плотности меди. 8875 кг/м3 — плотность шарика (ну просто масса, делённая на объём), а у меди — 8900 кг/м3.
А теперь проведём простую аналогию.
Пускай V — объём шарика сплошного, а V_o — полого.
Логично, что V \ \textgreater \ V_o (объём сплошного шара больше, чем у полого).
Тогда сравним плотности:
p_i = \frac{m_i}{V_i}.
Чем меньше объём, тем больше плотность. Следовательно у полого шарика плотность больше, чем у сплошного.
Вернёмся к нашей задаче. Пускай шарик полый, тогда его плотность больше, чем плотность меди. Но у нас у шарика плотность меньше, чем у меди. Следовательно полым он быть не может.
Имеем: g = 1,6 м/c²; T = 4,9 c. Найти: L - ?
1. Формула периода математического маятника: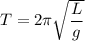 
.
2. Выразим длину: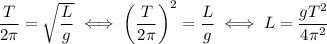 
.
3. Численно получим: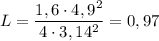 
(м).
Дано: C =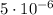 
Ф; T = 0,001 c. Найти: L - ?
1. Формула Томсона: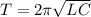 
.
2. Индуктивность из (1):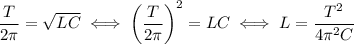 
.
3. Численно получим: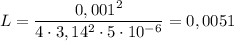 
(Гн).
4. Перевод: 0,0051 Гн = 5,1 мГн.
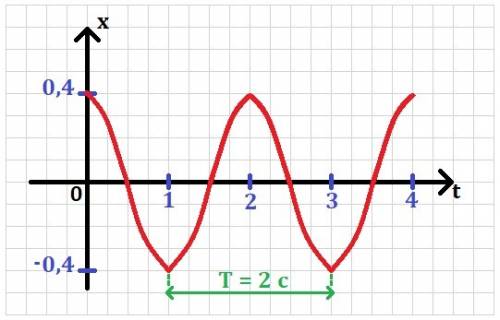
ответ: 5,1 мГн.======================Задача #3Имеем: x = 0,4cos(πt). Найти: A, T - ? Построить: x(t).
1. Уравнение гармонических колебаний в общем виде: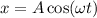 
, отсюда амплитуда A = 0,4 м и циклическая частота ω = π рад/с.
2. Формула циклической частоты: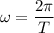 
, значит период: 
.
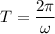3. Численно: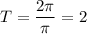 
(c).
График зависимости x(t) смотри в приложении.
