а измерения скорости
движения жидкости.
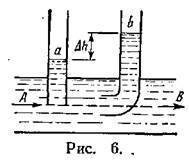
Представим, что в движущуюся жидкость опущены две трубки малого сечения, причем, плоскость поперечного сечения одной из них параллельна направлению скорости движения жидкости v, а другая (трубка Пито) изогнута так, что плоскость сечения изогнутой части
перпендикулярна направлению скорости течения (рис.6). Подъем жидкости в прямой трубке на высоту h1обусловлен лишь статическим давлением Рc, которое можно определить по формуле:
Pc= ρgh1.
В трубке Пито подъем жидкости на высоту h2обусловлен полным давлением Рп- в данном случае суммой статического Рси динамического Рддавлений (течение происходит горизонтально и весовое давление не учитывается). Следовательно:
Рп= Рс+ Рд;
ρgh2 = ρgh1 + ρv2/2
Из последней формулы находим линейную скорость жидкости:
.
Таким образом, по измеренной разности уровней жидкости в прямой и
изогнутой трубках определяется скорость течения жидкости. Этим же
методом определяют и скорость самолета относительно воздуха, катера относительно воды и др.
ответ: v=1,4 М\С
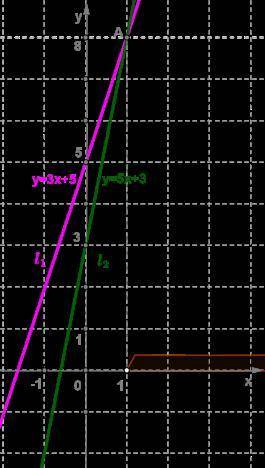
Для решения неравенства 3x+5<5x+3 построим графики линейных функций, расположенных в правой и левой части данного уравнения, т. е. построим графики y=3x+5 и y=5x+3.
Для построения графика каждой линейной функции составим таблицу значений.
Для функции y=3x+5 имеем:
x 0 1
y 5 8
Через полученные точки проведём прямую l1.
Для функции y=5x+3 имеем:
x 0 −1
y 3 −2
Через полученные точки проведём прямую l2.
Прямые y=3x+5 и y=5x+3 пересекаются в точке A(1;8). В этой точке значения функций равны.
Используя построение, делаем вывод: для того чтобы значение первой функции было меньше значения второй функции, необходимо, чтобы первый график был ниже второго, т. е. при x>1.
Можно проверить ответ, полученный при построении, решая неравенство:
3x+5<5x+3;3x−5x<3−5;−2x<−2;x>1.
Объяснение:
Ep2/Ep1 = (k2 Δx2²) / (k1 Δx1²)
Ep2/Ep1 = (40*10^(-4)) / (20*4*10^(-4)) = 0,5