Объяснение:
Задача 1
Дано:
m = 400 г = 400·10⁻³ кг
M = 20·10⁻³ кг/моль
i = 3 - число степеней свободы неона
t₁ = 17°C; T₁ = 17 + 273 = 290 К
t₂ = 117°C; T₂ = 117 + 273 = 390 К
______________________________
ΔU - ?
ΔU = (m/M)·(i/2)·R·ΔT
ΔU = (400/20)·(3/2)·8,31·(390-290) ≈ 25 кДж
Задача 2
Дано:
p - const
V = 20 м³
t₁ = 27°C; T₁ = 27 + 273 = 300 К
t₂ = 120°C; T₂ = 120 + 273 = 393 К
A = 500 кДж = 500 000 Дж
________________________
p - ?
По закону Гей-Люссака:
V₂ / V₁ = T₂/T₁
V₂ = V₁·(T₂/T₁) = 20·393/300 ≈ 26 м³
Работа:
A = p·ΔV
Давление:
p = A / ΔV = A / (V₂ - V₁) = 500 000 / (26 - 20) ≈ 83 кПа
Задача 3
Дано:
h = 60 м
η = 65%
с = 200 Дж / (кг·°С)
_________
Δt - ?
Потенциальная энергия:
Eп = m·g·h
Количество теплоты:
Q = η·A = η·m·g·h
Но:
Q = c·m·Δt
Приравняем:
c·m·Δt = η·m·g·h
Δt = η·g·h / c = 0,65·10·60 / 200 ≈ 2°C
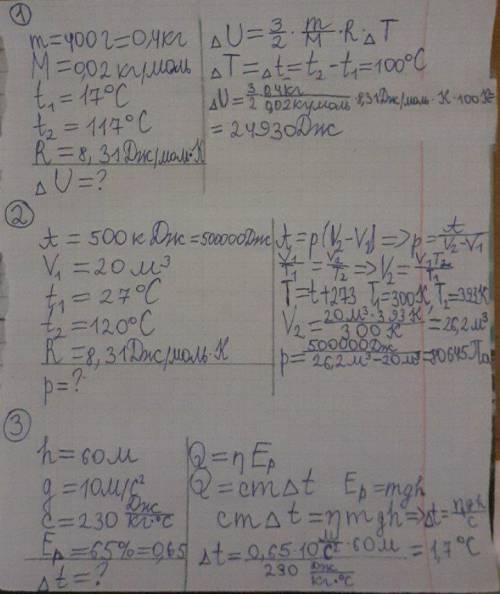
Дано:
ν = 5 моль
А = 831 Дж
Т2 = 22° С = 22 + 273 = 295 К
R = 8,31 Дж/(моль*К)
Т1 - ?
В изобарном процессе давление газа остаётся постоянным. Работа газа вычисляется по формуле:
А' = р*ΔV
Изменение объёма неизвестно, но мы можем выразить его через закон Гей-Люсака:
V1/T1 = V2/T2 - допустим, V2 известно, тогда V1 равно:
V1 = V2*(T1/T2) => ΔV = V2 - V1 = V2 - V2*(T1/T2) = V2*(1 - T1/T2)
Теперь просто выразим V2 из уравнения состояния газа:
рV2 = νRT2
V2 = νRT2/p
Подставляем всё в формулу работы газа, которая отрицательна, т.к. газ сжимается:
А' = -р*ΔV = -р*V2*(1 - T1/T2) = -р*(νRT2/p)*(1 - T1/T2) = -νRT2*(1 - T1/T2) = -νRT2 + νRT1 = νRT1 - νRT2
Тогда работа внешних сил положительна:
А = (-А') = νRT2 - νRT1
Выражаем Т1:
νRT2 - A = νRT1
(νRT2 - A)/(νR) = T1
T1 = T2 - A/(νR) = 295 - 831/(8,31*5) = 295 - 100/5 = 295 - 20 = 275 K
ответ: 275 К
В предложенных вариантах нет правильного ответа. Но 274 К вполне подходит.
следовательно, R также возрастет в 2 раза