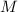= 10 кг -- максимально допустимая масса
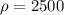кг/м³ -- плотность камня
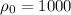кг/м³ -- плотность воды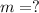
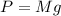. В воде на объект помимо силы тяжести будет действовать и выталкивающая сила Архимеда (направлена вверх, поэтому со знаком минус): 
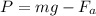. Именно поэтому в воде проще поднимать тяжелые предметы. Сила Архмеда определяется следующим образом:
,
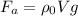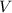- объем тела, а 
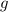- ускорение свободного падения. Объем тела является отношением массы тела 
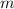к плотности тела 
: 
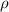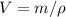. Таким образом, можем определить вес предмета в воде так:
.
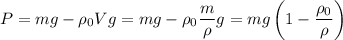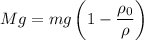
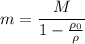
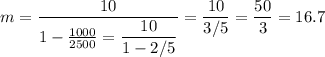кг.
Объяснение:
Второй закон термодинамики устанавливает критерии необратимости термодинамических процессов. Известно много формулировок второго закона, которые эквивалентны друг другу. Мы приведем здесь только одну формулировку, связанную с энтропией.
Существует функция состояния - энтропия S, которая обладает следующим свойством: , (4.1) где знак равенства относится к обратимым процессам, а знак больше - к необратимым.
Для изолированных систем второй закон утверждает: dS і 0, (4.2) т.е. энтропия изолированных систем в необратимых процессах может только возрастать, а в состоянии термодинамического равновесия она достигает максимума (dS = 0,
d 2S < 0).
Неравенство (4.1) называют неравенством Клаузиуса. Поскольку энтропия - функция состояния, ее изменение в любом циклическом процессе равно 0, поэтому для циклических процессов неравенство Клаузиуса имеет вид:
, (4.3)
где знак равенства ставится, если весь цикл полностью обратим.
Энтропию можно определить с двух эквивалентных подходов - статистического и термодинамического. Статистическое определение основано на идее о том, что необратимые процессы в термодинамике вызваны переходом в более вероятное состояние, поэтому энтропию можно связать с вероятностью:
, (4.4)
где k = 1.38 10-23 Дж/К - постоянная Больцмана (k = R / NA), W - так называемая термодинамическая вероятность, т.е. число микросостояний, которые соответствуют данному макросостоянию системы (см. гл. 10). Формулу (4.4) называют формулой Больцмана.
С точки зрения строгой статистической термодинамики энтропию вводят следующим образом:
, (4.5)
где G (E) - фазовый объем, занятый микроканоническим ансамблем с энергией E.
Термодинамическое определение энтропии основано на рассмотрении обратимых процессов:
. (4.6)
Это определение позволяет представить элементарную теплоту в такой же форме, как и различные виды работы:
Qобр = TdS, (4.7)
где температура играет роль обобщенной силы, а энтропия - обобщенной (тепловой) координаты.
Расчет изменения энтропии для различных процессов
Термодинамические расчеты изменения энтропии основаны на определении (4.6) и на свойствах частных производных энтропии по термодинамическим параметрам:
(4.8)
Последние два тождества представляют собой соотношения Максвелла (вывод см. в гл. 5).
1) Нагревание или охлаждение при постоянном давлении.
Количество теплоты, необходимое для изменения температуры системы, выражают с теплоемкости: Qобр = Cp dT.
(4.9)
Пример 4-3. Найдите изменение энтропии газа и окружающей среды, если n молей идеального газа расширяются изотермически от объема V1 до объема V2: а) обратимо; б) против внешнего давления p.
