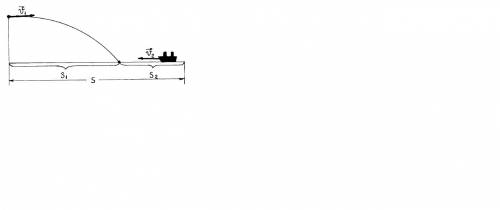
F=mg,где m-масса космонавта,а g-ускорение свободного падения,но так как у нас разные планеты,то и g будет различным.Найдём g по формуле g=GM/(R^2),где G-гравитационна постоянная, M и R -масса и радиус планеты
g земли=G*M(з)/(R(з)^2)
по условию масса марса=0.5M(з),а радиус марса=R(з)/2,тогда
g марса=G*M(з)/ (2.5*(R (з))^2)
подставим ускорения свободного падения в формулу F=mg,найдём отношение F(з)/F(м)
F(з)/F(м)=m*G*M(з)*2.5*(R(з))^2/((R(з))^2*m*G*M(з))
F(з)/F(м)=2.5,следовательно F(м)= F(з)/2.5=700/2.5=280(H)
ответ:4) 280 Н
Для начала всё выразим в систему СИ: 180 км/ч = 50 м/с; 24 км/ч ≈ 6,67 м/с.
Тело падающее с определёной высоты, в любом направлении, будет падать одно и тоже время относительно траектории его бросания т.е иными словами: если тело падает с какой-то высоты (в данном случае 500 метро), то это тело брошенное не важно как, вертикально вниз или горизонтально, под углом 60°, под углом 11°, не важно как, это тело будет падать во всех случаях одинаково, вернее за одинаковое время.
Смотрим 20ой ресунок.
Траектория движения вымпела - парабола. S₁ - расстояние пройденое вымпелом в горизонтальном направлении, S₂ - путь пройденый теплоходом.
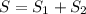(необходимо определить)
Движение вымпела в горизонтальном направлении равномерное, в вертикальном направлении равноускоренное, при этом на вымпел действует постоянная сила тяжести.
Путь пройденный вымпелом: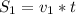 
(1)
Так как время движения вымпела в горизонтальном и вертикальном направлении одинаково то выполняется условие: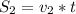 
(2) (путь пройденный теплоходом).
По условию задачи вертолёт двигается со скоростью 180 км/ч или же 50 м/с, переносит вымпел. После бросания вымпела с вертолёта, вымпел будет двигатся по парабалической траекторией. При этом вымпел будет падать за определёный промежуток времени. По формуле высоты с которой падает тело за время "t"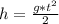 
, где g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²), t - промежуток времени (с). Из данной формулы выражаем время в течении которого будет падать вымпел: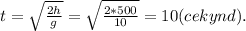 
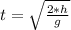. Высота равна 500 метров (по условию), тогда подставляем и вычисляем: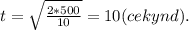 
Использую формулы (1) и (2) получим: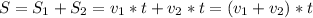 
Подставляем численные данные и вычисляем:
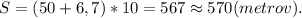
ответ: 570 метров.
