5 с
Объяснение:
Запишем уравнение движения Фокса и Форда, приняв для последнего начальную координату за x₀₂ и скорость за v₂:
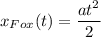
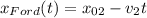
Тогда, расстояние между ними подчиняется закону:
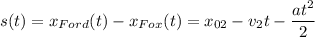
По условию, в некоторый момент времени τ это расстояние удовлетворяет условию:
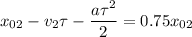
Скорости Фокса и Форда:
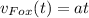
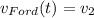
Их относительная скорость в момент времени τ:
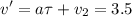 м/с
м/с
Подставляя все исходные данные в уравнения получим систему:
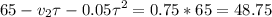
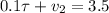
Выражаем скорость Форда из второго уравнения и подставляем ее в в первое:
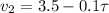
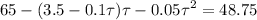
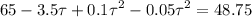
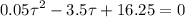
Решая полученное квадратное уравнение, находим два корня 65 и 5 секунд. Скорости Форда, соответствующие этим временам 3,5-0,1*5=3 м/с и 3,5-0,1*65=-3 м/с, значит нам подходит решение 5 секунд, так как для 65 секунд Форд идет не на встречу Фоксу, а убегает от него.
5 с
Объяснение:
Запишем уравнение движения Фокса и Форда, приняв для последнего начальную координату за x₀₂ и скорость за v₂:
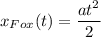
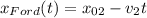
Тогда, расстояние между ними подчиняется закону:
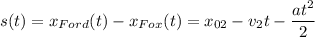
По условию, в некоторый момент времени τ это расстояние удовлетворяет условию:
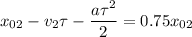
Скорости Фокса и Форда:
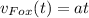
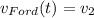
Их относительная скорость в момент времени τ:
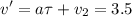 м/с
м/с
Подставляя все исходные данные в уравнения получим систему:
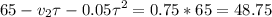
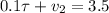
Выражаем скорость Форда из второго уравнения и подставляем ее в в первое:
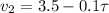
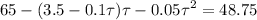
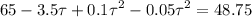
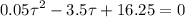
Решая полученное квадратное уравнение, находим два корня 65 и 5 секунд. Скорости Форда, соответствующие этим временам 3,5-0,1*5=3 м/с и 3,5-0,1*65=-3 м/с, значит нам подходит решение 5 секунд, так как для 65 секунд Форд идет не на встречу Фоксу, а убегает от него.
35.26*C
Объяснение:
Количество теплоты при нагревании тела вычисляется по формуле:
Сколько тело отдаст Дж, столько вода и примет. Так же до какой температуры вода нагреется, до такой же тело остынет. Значит верно равенство:
Минус ставим после знака равно, т.к. тело остывает.
Опускаем второе (полностью аналогичное первому) тело. Теперь нагревается не только вода, но и первое тело, а второе остывает. Начальная температура воды такая же, как и начальная температура первого тела, т.е. 25*C. Когда установится тепловое равновесие, все три тела станут одинаковой температуры, т.е. tk. Поэтому справедливо утверждать:
Объеденим выражения в систему:
Поделим первую строку на вторую: