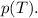Решение писал для себя, чтобы легче решать было
1.Q=cm(t2-t1)
3600Дж=c*0,2кг*(200°-150°)
c=3600/0,2*50°=360 Дж/кг*C°
2.Q=0,04кг*88.000Дж/кг(не знаю как на клаве символ теплоты плавления пишется,поэтому сразу цифрами)
Q=3520 Дж
3.n*m2*q=c*m*(t2-t1)+z*m
Где
n=50%=0,5 (КПД)
m2=2500 кг(масса угля)
q=27.000.000 Дж/кг
c=500 Дж/кг*C°
m=?(масса стали)
t2=1500°(конечная температура
t1=200°(начальная температура)
z=84000 Дж/кг(удельная теплота плавления стали,обозначается другой буквой)
n*m2*q=m*(c*(t2-t1)+z)(массу стали вынесли за скобки
m=n*m2*q/c*(t2-t1)+z
m=0,5*2500*27.000.000/500*1300°+84.000=45980,9264 кг
4.n=Q1-Q2/Q1=60/80=0,75
n=75%
А=60 кДж=60000 Дж
1. Дано:
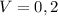 м³
м³
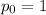 атм
атм 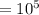 Па
Па

 атм
атм 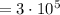 Па
Па
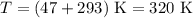
Найти: 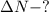
Решение. Применим закон Авогадро: в равных объемах газов при одинаковых температурах и давления содержится одинаковое количество молекул:
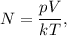
где 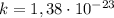 Дж/К — постоянная Больцмана.
Дж/К — постоянная Больцмана.
Поскольку объем газа не изменяется, то есть имеем изохорный процесс: 
Определим количество молекул в начале:
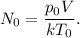
Определим количество молекул в конце:

Тогда число молекул газа изменилось на:
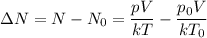
Определим значение искомой величины:
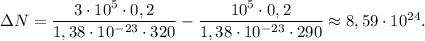
ответ: число молекул увеличилось на 
2. Дано:
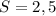 см²
см² 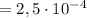 м²
м²

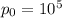 Па
Па

Найти: 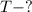
Решение. Поскольку бутылку закрыли плотно, то объем газа не изменяется. Значит, имеем изохорный процесс. Изохорный процесс описывается законом Шарля: для данной массы газа отношение давления газа к его температуре является постоянным, если объем газа не меняется:
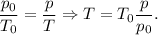
Сила давления — сила, действующая перпендикулярно к поверхности:
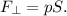
Поскольку сила трения — это внешняя сила, то ее значение равно произведению изменения давления на площадь поперечного сечения пробки:
 , откуда
, откуда 
Значит,
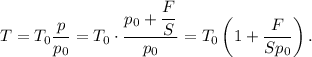
Определим значение искомой величины:
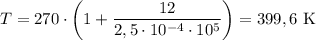
ответ: 400 К.
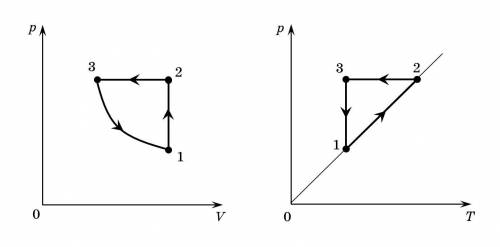
3. Имеем циклический процесс макроскопических параметров. Здесь:
 — изохорное нагревание;
— изохорное нагревание;
 — изобарное охлаждение;
— изобарное охлаждение;
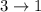 — изотермическое расширение.
— изотермическое расширение.
Изобразим этот процесс в координатах 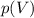 и
и