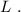 Пусть передъ тѣмъ, какъ передняя точка локомотива равняется съ наблюдателемъ – поѣздъ неограниченное время ужѣ ѣдетъ съ тѣмъ же ускореніемъ. За начало отсчета времени примемъ тотъ моментъ, когда скорость поѣзда была равна нулю. Въ такомъ случаѣ уравненіе движенія поѣзда упростится и не будетъ содержать начальной скорости, однако, когда передняя точка локомотива поравняется съ наблюдателемъ – поѣздъ ужѣ проѣдетъ нѣкоторое разстояніе
Пусть передъ тѣмъ, какъ передняя точка локомотива равняется съ наблюдателемъ – поѣздъ неограниченное время ужѣ ѣдетъ съ тѣмъ же ускореніемъ. За начало отсчета времени примемъ тотъ моментъ, когда скорость поѣзда была равна нулю. Въ такомъ случаѣ уравненіе движенія поѣзда упростится и не будетъ содержать начальной скорости, однако, когда передняя точка локомотива поравняется съ наблюдателемъ – поѣздъ ужѣ проѣдетъ нѣкоторое разстояніе 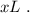
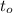 въ это мгновеніе можно выразить, какъ:
въ это мгновеніе можно выразить, какъ: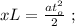
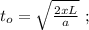 [1]
[1]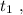 когда проѣдетъ локомотивъ:
когда проѣдетъ локомотивъ: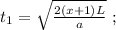
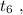 когда проѣдетъ почти вѣсь поѣздъ, но всё жъ пока-таки безъ шести вагоновъ:
когда проѣдетъ почти вѣсь поѣздъ, но всё жъ пока-таки безъ шести вагоновъ: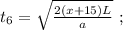
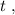 когда въ концѣ концовъ проѣдетъ вѣсь поѣздъ:
когда въ концѣ концовъ проѣдетъ вѣсь поѣздъ: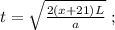 [2]
[2]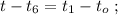
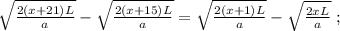
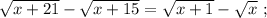
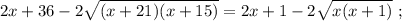
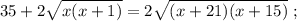
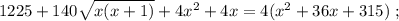
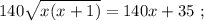
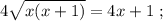
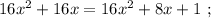
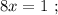
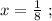
 ужѣ и слѣдуетъ отвѣтъ на вопросъ задачи:
ужѣ и слѣдуетъ отвѣтъ на вопросъ задачи: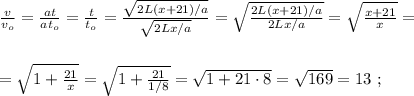
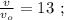
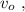

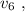
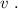
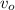 до
до  и от состояния
и от состояния  до
до  – одинаковы, а значит и изменение скорости одинаковое, поскольку движение равноускоренное:
– одинаковы, а значит и изменение скорости одинаковое, поскольку движение равноускоренное: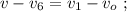 [1]
[1] до
до  – поезд проезжает расстояние вшестеро большее, чем от состояния
– поезд проезжает расстояние вшестеро большее, чем от состояния 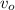 до
до 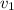 – а значит, средняя скорость
– а значит, средняя скорость  вшестеро больше средней скорости
вшестеро больше средней скорости 
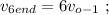
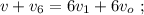
 [2]
[2]
 вагонов + локомотив.
вагонов + локомотив.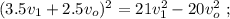
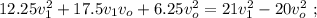
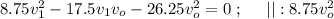
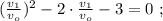
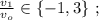
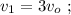
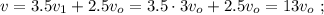

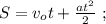
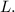
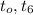 и
и 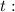
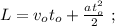 [1]
[1] [2]
[2]
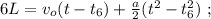
 то, используя [1]:
то, используя [1]:

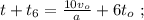
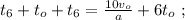
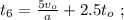
 [3]
[3]


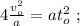
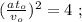
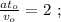

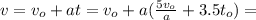
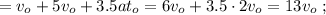

Примеров равномерного движения в природе очень мало. Почти равномерно движется вокруг Солнца Земля, капают капли дождя, всплывают пузырьки в газировке. Даже пуля, выпущенная из пистолета, движется прямолинейно и равномерно только на первый взгляд. От трения о воздух и притяжения Земли полет ее постепенно становится медленнее, а траектория снижается. Вот в космосе пуля может двигаться действительно прямолинейно и равномерно, пока не столкнется с каким-либо другим телом. А с неравномерным движением дело обстоит куда как лучше – примеров множество. Полет мяча во время игры в футбол, движения льва, охотящегося на добычу, путешествия жвачки во рту семиклассника и бабочки, порхающей над цветком, – все это примеры неравномерного механического движения тел.