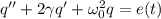, полученным из уравнения Кирхгофа введением обозначений: 
, 
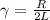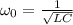. Для выяснения резонансной частоты возьмем вынуждающую силу, изменяющуюся по закону косинуса. 
.
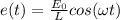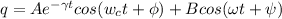, где первое слагаемое - решение с.о.у. (оно затухает и нас не интересует), а второе - произвольное частное решение, которое ищется в указанном виде (в силу особенностей взятой вынуждающей силы). Подставим решение 
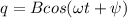в уравнение и (с например, векторной диаграммы) получим 
.
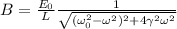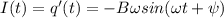и 
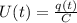. Получаем для амплитуды тока и напряжений следующие выражения: 
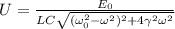и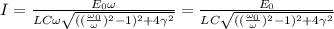 
.
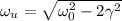, а у тока при 
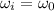.![q = Ae^{-\gamma t}cos(w_c t + \phi)[\tex] Условились считать, что колебание затухло, если его амплитуда уменьшилась в e раз. Очевидно, что это произойдёт за время [tex]\tau = \frac{1}{\gamma}](/tpl/images/0411/3944/118a7.png)
. За это время система совершила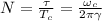 
колебаний, где 
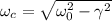- собственная частота колебаний системы (следует из решения д.у.). Так вот, величина 
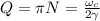называется добротностью контура.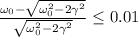
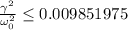, отсюда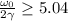 
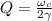и ![\frac{\omega_0}{2\gamma}[\tex] разные величины, поэтому оценим погрешность, что бы приравнять их с чистой совестью)))) Для этого разложим выражение для добротности, с учётом определения частоты собственных колебаний по формуле Маклорена (в ряд). [tex]Q = \frac{ \sqrt{\omega_0^2 - \gamma^2}}{2\gamma} = \frac{\omega_0}{2\gamma} \sqrt{1 - \frac{\gamma^2}{\omega_0^2}} = \frac{\omega_0}{2\gamma} ( 1 - \frac{\gamma^2}{2\omega_0^2} + o(\frac{\gamma^2}{\omega_0^2})) = \frac{\omega_0}{2\gamma} - \frac{\gamma}{4\omega_0} + o(\frac{\gamma}{\omega_0}).](/tpl/images/0411/3944/feb4a.png)
Таким образом, отличие истинного решения от полученного примерно 0.03.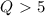
Eк1-Fтр*S=Eк2
m*(V1^2-V2^2)/2=k*m*g*S
k=(V1^2-V2^2)/2*g*S=(100-64)/36*20=0.05 - ответ
2) дано p1=11.35 p2=7.8 г/см3 v1=v2 V1=V2
P=m*V=p*v*V
P1/P2=p1/p2=1.455