тогда мы можем выразить время, которое тратит жук на прохождение расстояния между 
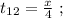
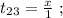
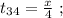
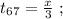
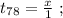
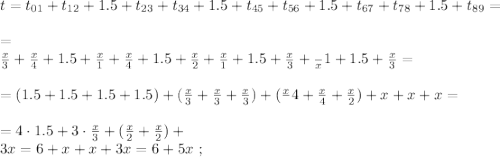
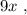поскольку мы изначальнго определили как цену деления линейки Глюка. Стало быть:
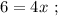
см
ПОСТАВЬ КОРОНУ
1)Физи́ческий ма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Содержание
1 Дифференциальное уравнение движения физического маятника
2 Центр качания физического маятника
2.1 Теорема Гюйгенса
2.1.1 Формулировка
2.1.2 Доказательство
3 Период колебаний физического маятника
3.1 Период малых колебаний физического маятника
4 См. также
5 Ссылки
Дифференциальное уравнение движения физического маятника
Физический маятник.
{\displaystyle O}O — ось подвеса;
{\displaystyle N}N — реакция оси подвеса;
{\displaystyle G}G — центр тяжести;
{\displaystyle O'}O' — центр качания;
{\displaystyle \lambda }\lambda — приведённая длина;
{\displaystyle \theta }\theta — угол отклонения маятника от равновесия;
{\displaystyle \alpha }\alpha — начальный угол отклонения маятника;
{\displaystyle m}m — масса маятника;
{\displaystyle h}h — расстояние от точки подвеса до центра тяжести маятника;
{\displaystyle g}g — ускорение свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса по теореме Штайнера:
{\displaystyle I=I_{0}+mh^{2}=m\left(r^{2}+h^{2}\right),}{\displaystyle I=I_{0}+mh^{2}=m\left(r^{2}+h^{2}\right),}
где {\displaystyle I_{0}}I_0 — момент инерции относительно оси проходящей через центр тяжести;
{\displaystyle r}r — эффективный радиус инерции относительно оси, проходящей через центр тяжести.
Динамическое уравнение произвольного вращения твёрдого тела:
