ответ: 10 г
Объяснение:
Дано:
М = 240 г = 0,24 кг
s = 160 см = 1,6 м
t = 4 c
--------------------------------
m - ?
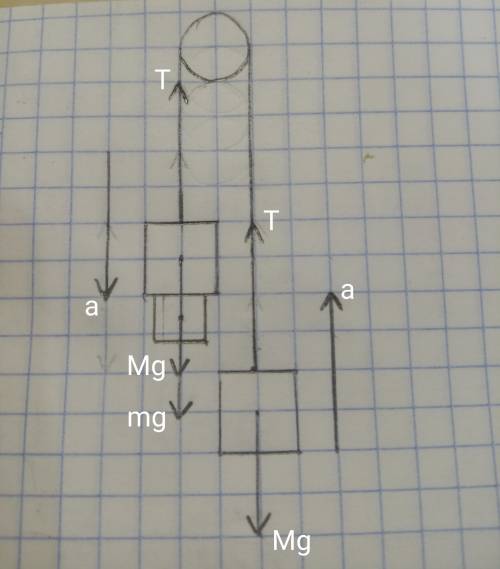
Допустим дополнительный груз мы прикрепили к телу находящиегося слева
Теперь запишем второй закон Ньютона для обоих тел и составим систему
( M + m )a = ( M + m )g - T
Ma = T - Mg
Решим систему методом сложения
( 2M + m )a = ( M + m )g - Mg
( 2M + m )a = Mg + mg - Mg
( 2M + m )a = mg
2Ma + ma = mg
2Ma = m( g - a )
m = ( 2Ma )/( g - a )
Так так как оба блока отпустили без начальной скорости
Тогда s = ( at² )/2
a = ( 2s )/t²
a = ( 2 * 1,6 )/4² = 0,2 м/с²
Значит
m = ( 2 * 0,24 * 0,2 )/( 10 - 0,2 ) ≈ 10 г
уравнение равноускоренного движения:
x(t) = x₀ + V₀ * t + (a * t²) / 2
начальная скорость и начальное положение тела равны 0, следовательно x(t) = (a * t²) / 2
чтобы найти ускорение решим уравнение:
x(5с) - x(4с) = 0.9м
(a * (5с)²) / 2 - (a * (4с)²) / 2 = 0.9м
a * 25с² - a * 16с² = 1.8м
a * 9c² = 1.8м
a = 1.8м / 9c² = 0.2м/с²
с известным ускорением найдем перемещение тела за 7-ю секунду:
x(7с) - x(6с) = (a * (7с)²) / 2 - (a * (6с)²) / 2 = (a / 2) * ((7с)² - (6с)²) = 0.1м/с² * 13c² = 1.3м
ответ: 130см.
В нашей задаче в любой момент времени на шесте имеется такая точка, скорость которой направлена только вдоль шеста и не имеет проекции, перпендикулярной шесту. Это точка касания шеста и угла крыши. Значит, движение шеста можно представить как сумму перемещения параллельно себе и вращения вокруг именно этой точки.
Когда шест касается крыши сарая своей серединой, его концы равноудалены от центра этого вращения, следовательно модули составляющих скоростей концов стержня, перпердикулярные стержню, тоже равны.
Таким образом получаем, что у концов стержня равны модули и касательных и нормальных к стержню составляющих, значит скорости концов равны по модулю
ответ v0