на электрон, находящийся в электрическом поле, действует электрическая сила \( модуль которой мы определим таким образом:
\[f = ee\]
здесь \(e\) — модуль заряда электрона (элементарный заряд), равный 1,6·10-19 кл. напряженность поля между пластинами \(e\) связана с напряжением \(u\) и расстоянием между пластинами \(d\) следующей формулой:
\[e = \frac{u}{d}\]
тогда имеем:
\[f = \frac{{ue}}{d}\]
работу электрического поля \(a\) по перемещению заряда на расстояние \(s\) найдём так:
\[a = fs\]
\[a = \frac{{ues}}{d}\; \; \; \; (
также работу поля можно определить как изменение кинетической энергии электрона. так как = то:
\[a = \frac{{{m_e}{\upsilon ^2}}}{2}\; \; \; \; (
здесь \(m_e\) — масса электрона, равная 9,1·10-31 кг. теперь приравняем (1) и (2), тогда получим:
{{{m_e}{\upsilon ^2}}}{2} = \frac{{ues}}{d}\]
нам осталось только выразить искомую скорость ):
= \sqrt {\frac{{2ues}}{{{m_e}d}}} \]
произведём вычисления:
= \sqrt {\frac{{2 \cdot 120 \cdot 1,6 \cdot {{10}^{ — 19}} \cdot 0,003}}{{9,1 \cdot {{10}^{ — 31}} \cdot 0,02}}} = 2,52 \cdot {10^6}\; м/с = 2520\; км/с\]
Дано:
------------------------------
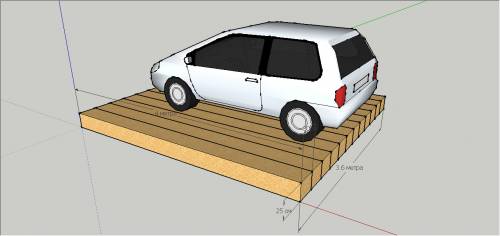
V(плот)=3.6 м³ (находим так: 4м × 0.25м × 0.3м × 12 брусьев)
P(авто)=10000 Н
ρ(ель)=430 кг/м³
ρ(вода)=1000 кг/м³
g=9.8 Н/кг
------------------------------
Найти:
Fa > P(плот) + P(авто) ?
Другими словами: можно ли на этом плоту переправить через реку автомобиль, не потопив при этом плот с грузом. Будет ли Архимедовой силы от воды достаточно, чтобы удерживать плот на поверхности воды, или нет?
------------------------------
Решение:
Вначале начертим графически задачу, смотри катинку.
m(плот)=V(плот) × ρ(ель) = 3.6 м³ × 430 кг/м³ = 1548 кг
P(плот)=m(плот) × g = 1548 кг × 9.8 Н/кг = 15170.4 Н
P(плот) + P(авто) = 10000 Н + 15170.4 Н = 25170.5 Н
Теперь найдём какая сила выталкивания будет действовать на плот, если его полностью погрузить в воду.
Fa = V(плот) × ρ(вода) × g = 3.6 м³ × 1000 кг/м³ × 9.8 Н/кг = 35280 Н
Имеем:
35280 Н > 25170.5 Н, тоесть Fa > P(плот) + P(авто)
ответ: Можно
m=p*V,где р-плотность,V-объем.
m=1100 кг/м3*0.000045 м3=0,0495 кг