1.
Если груз 2 движется вверх, то m₁ ≈ 0.171 кг .
Если груз 2 движется вниз, то m₁ ≈ 0.933 кг .
2.
Время движения равно 10 с.
Объяснение:
1.
а = 4 м/с²
m₂ = 0.4 кг
g = 10 м/с²
m₁ - ?
Т - ?
Допустим, что груз 2 движется вниз Груз 2 движется вверх
Уравнение движения Уравнение движения
m₂а = m₂g - Т m₂а = -m₂g + Т
откуда откуда
Т = m₂(g - a) = 0.4·(10 - 4)=2.4 (H) Т = m₂(g +a) = 0.4·(10 + 4) = 5,6 (H)
Груз 1 движется вверх Груз 1 движется вниз
m₁a = T - m₁g m₁a = -T + m₁g
откуда откуда
m₁ =T: (a + g)= 2.4:(4 + 10) ≈ 0.171 (кг) m₁ =T:(g - a)= 5.6:(10 -4) ≈ 0.933 (кг)
2.
m = 1 т = 1000 кг
Fт = 2,5 кН = 2500 Н
s = 100 м
v₀ = 0
μ = 0.05
g = 10 Н/кг
t - ?
Сила cопротивления движению равна
Fc = mgμ = 1000 · 10 · 0.05 = 500 (Н)
По 2-му закону Ньютона
ma = Fт - Fс
откуда ускорение автомобиля
а = (Fт - Fс) : m = (2500 - 500) : 1000 = 2 (м/с²)
При равноускоренном движении из состояния покоя путь равен
s = 0.5 at²
откуда время движения
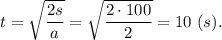
Пример 1. Определить реакции опор горизонтальной балки от заданной нагрузки.
Дано:
Схема балки (рис. 1).
P = 20 кН, G = 10 кН, М = 4 кНм, q = 2 кН/м, a=2 м, b=3 м, .
Определить реакции опор в точках А и В.

Рис. 1
Рассмотрим равновесие балки АВ (рис. 2).
К балке приложена уравновешенная система сил, состоящая из активных сил и сил реакции.
Активные (заданные) силы:
, , , пара сил с моментом М, где
- сосредоточенная сила, заменяющая действие распределенной вдоль отрезка АС нагрузки интенсивностью q.
Величина

Линия действия силы  проходит через середину отрезка АС.
Силы реакции (неизвестные силы):
, , .
 - заменяет действие отброшенного подвижного шарнира (опора А).
Реакция  перпендикулярна поверхности, на которую опираются катки подвижного шарнира.
,  - заменяют действие отброшенного неподвижного шарнира (опора В).
,  - составляющие реакции , направление которой заранее неизвестно.