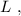 и жёсткостью
и жёсткостью 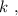 деформацию которой обозначим, как
деформацию которой обозначим, как 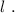 Тогда возникающая сила упругости при её деформации будет выражаться обычным законом Гука:
Тогда возникающая сила упругости при её деформации будет выражаться обычным законом Гука: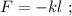
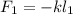
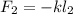

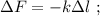
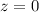 – все силы, действующие на груз, взаимно скомпенсированы. При изменении положения груза на
– все силы, действующие на груз, взаимно скомпенсированы. При изменении положения груза на 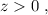 (т.е. вверх), растяжение нижней пружины (down) увеличится, а значит её сила, действующая на груз вниз – тоже увеличится по модулю. В проективном виде это изменение выразится, как:
(т.е. вверх), растяжение нижней пружины (down) увеличится, а значит её сила, действующая на груз вниз – тоже увеличится по модулю. В проективном виде это изменение выразится, как: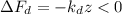 – это символизирует увеличение отрицательной (направленной вниз) величины силы нижней пружины.
– это символизирует увеличение отрицательной (направленной вниз) величины силы нижней пружины.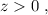 (вверх), растяжение верхней пружины (up) уменьшится, а значит её сила, действующая на груз вверх – тоже уменьшится по модулю. В проективном виде это изменение выразится, как:
(вверх), растяжение верхней пружины (up) уменьшится, а значит её сила, действующая на груз вверх – тоже уменьшится по модулю. В проективном виде это изменение выразится, как: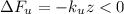 – это символизирует уменьшение положительной (направленной вверх) величины силы верхней пружины.
– это символизирует уменьшение положительной (направленной вверх) величины силы верхней пружины.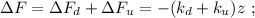
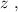 общая сила, действующая со стороны системы пружин – будет как раз и равна изменению действующих сил:
общая сила, действующая со стороны системы пружин – будет как раз и равна изменению действующих сил: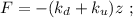
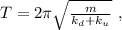 где
где 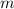 – масса шарика.
– масса шарика.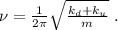
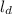 (нижней), и
(нижней), и 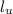 (верхней). При этом положим вертикальное положение груза
(верхней). При этом положим вертикальное положение груза  Ось
Ось 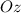 направлена вверх.
направлена вверх.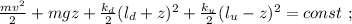
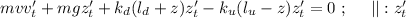
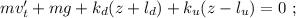
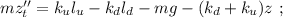
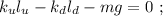
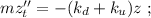
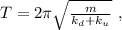 где
где 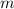 – масса шарика.
– масса шарика.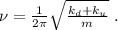
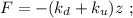
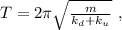 где
где 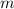 – масса шарика.
– масса шарика.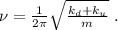
 Н/см
Н/см 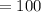 Н
Н 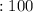 см
см 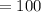 Н
Н 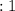 м
м 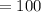 Н/м ;
Н/м ;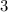 Н/см
Н/см 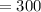 Н
Н 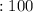 см
см 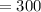 Н
Н 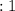 м
м 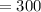 Н/м ;
Н/м ;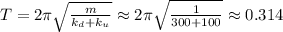 сек ;
сек ;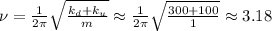 Гц .
Гц .
η=0.3
Qн=80000 Дж
Найти:
Qх-? Дж
Решение:
η(КПД)=(Qн-Qх)/Qн, где Qн-теплота, переданная газу нагревателем, Qх-теплота, переданная холодильнику;
Qн-Qх=η*Qн; Qн-Qx=0.3*80000=24000 Дж
Qх=Qн-24000; Qх=80000-24000=56000 Дж
ответ: Qх=56000 Дж