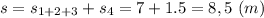
0 кг и радиусом R = 5 см вращался с
частотой n = 8 с-1. К цилиндрической поверхности вала прижали
тормозную колодку с силой F = 40 Н, под действием которой вал
остановился через t = 10 с. Определить коэффициент трения f.
3.13. На цилиндр намотана тонкая гибкая нерастяжимая
лента, массой которой по сравнению с массой цилиндра можно
пренебречь. Свободный конец ленты прикрепили к кронштейну и
предоставили цилиндру опускаться под действием силы тяжести.
Определить линейное ускорение а оси цилиндра, если цилиндр:
1) сплошной; 2) полый тонкостенный.
3.14. Через блок, имеющий форму диска, перекинут шнур. К
концам шнура привязаны грузики массой m1 = 100 г и m2 = 110 г.
С каким ускорением а будут двигаться грузики, если масса m
блока равна 400 г? Трение при вращении блока ничтожно мало.
3.15. Два тела массами m1 = 0,25 кг и m2 = 0,15 кг связаны
тонкой нитью, переброшенной через блок. Блок укреплён на краю
Пройденный путь 8,5 м; модуль перемещения 2,5 м;
1-й этап движения
t₀ = 0; v₀ = 2 м/с;
t₁ = 1 с; v₁ = 3 м/с
Расчёт:
Δt₁ = t₁ - t₀ = 1 - 0 = 1 (c);
Δv₁ = v₁ - v₀ = 3 - 2 = 1 (м/c);
На 1-м этапе движение равноускоренное с ускорением
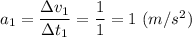
по закону
x₁(t) = 2t + 0.5t²
Считаем, что в начальный момент движения координата x₁(0) = 0
В момент времени t₁ = 1 c координата x₁(1) = 2·1 + 0.5·1² = 2.5 (м)
Движение происходит в сторону увеличения координаты.
Перемещение
r₁ = x₁(1) - x₁(0) = 2.5 - 0 = 2.5 (м)
Пройденный путь за этап
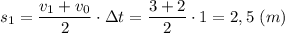
2-й этап движения
t₁ = 1 с; v₁ = 3 м/с
t₂ = 3 с; v₂ = 0;
Расчёт:
Δt₂ = t₂ - t₁ = 3 - 1 = 2 (с);
Δv₂ = v₂ - v₁ = 0 - 3 = -3 м/c;
На 2-м этапе движение равнозамедленное с ускорением
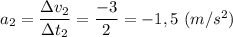
по закону
x₂(t) = 2.5 + 3 · (t - t₁) - 0.75 · (t - t₁)²
В момент времени t₂ = 3 c координата
x₂(3) = 2.5 + 3 · 2 - 0.75 · 2² = 5.5 (м)
Движение происходит в сторону увеличения координаты.
Перемещение к концу этапа
r₂ = x₂(3) - x₁(0) = 5.5 - 0 = 5.5 (м)
Пройденный путь за этап
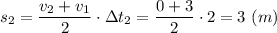
Пройденный путь за 2 этапа
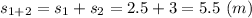
3-й этап движения
t₂ = 3 с; v₂ = 0;
t₃ = 6 с; v₃ = -1 м/с
Расчёт:
Δt₃ = t₃ - t₂ = 6 - 3 = 3 (с);
Δv₃ = v₃ - v₂ = -1 - 0 = -1 м/c;
На 3-м этапе движение равноускоренное с ускорением
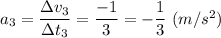
по закону
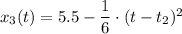
В момент времени t₃ = 6 c координата
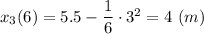
Движение происходит в сторону уменьшения координаты.
Перемещение к концу этапа
r₃ = x₃(6) - x₁(0) = 4 - 0 = 4 (м)
Пройденный путь за этап
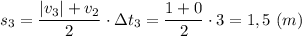
Пройденный путь за 3 этапа
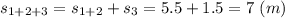
4-й этап движения
t₃ = 6 с; v₃ = -1 м/с
t₄ = 9 с; v₄ = 0;
Расчёт:
Δt₄ = t₄ - t₃ = 9 - 6 = 3 (с);
Δv₄ = v₄ - v₃ = 0 + 1 = 1 м/c;
На 3-м этапе движение равнозамедленное с ускорением
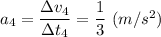
по закону
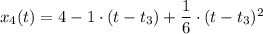
В момент времени t₄ = 9 c координата
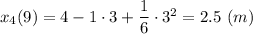
Движение происходит в сторону уменьшения координаты.
Перемещение к концу этапа
r₄ = x₄(9) - x₁(0) = 2.5 - 0 = 2.5 (м)
Пройденный путь за этап

Путь, пройденный за всё время движения