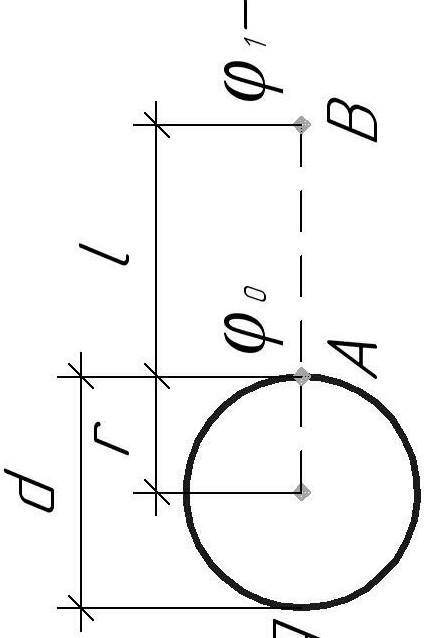
Дано: d=30 см, φ0=5400 В, l=15 см, φ1−?
Потенциал φ0 на поверхности сферы (то есть в точке
A) радиусом r, имеющей некоторый заряд q, определим по формуле:
φ0=kqr
Так как радиус сферы равен половине диаметра (r=d2), то имеем:
φ0=2kqd(1)
Потенциал φ1 на расстоянии l от поверхности сферы (в точке B) можно найти из формулы:
φ1=kqr+l
Учитывая, что r=d2, получим:
φ1=kqd2+l
Домножим и числитель, и знаменатель на 2:
φ1=2kqd+2l(2)
Теперь поделим (2) на (1):
φ1φ0=dd+2l
В итоге получим такое решение:
φ1=φ0dd+2l
Посчитаем численный ответ:
φ1=5400⋅0,30,3+2⋅0,15=2700В
ответ:2700В
Дырочная проводимость
Объяснение:
Введем в кристалл кремния трехвалентный атом индия (In). Индий установит ковалентные связи лишь с тремя соседними атомами кремния. Для четвертого «соседа», у индия не хватает одного электрона. Этот недостающий электрон может быть захвачен атомом индия из ковалентной связи соседних атомов кремния.
Атом индия превратиться в негативно заряженный ион, а в ковалентной связи соседних атомов образуется вакансия (дырка). В свою очередь, на это место может перескочить электрон из соседней ковалентной связи. В результате получается хаотическое блуждание дырок по кристаллу.
Если поместить полупроводник в электромагнитное поле, движение дырок станет упорядоченным, т.е. возникнет электрический ток. Таким образом, обеспечивается дырочная проводимость. Полупроводник с дырочной проводимостью называется полупроводником P-типа.
Fтяги - Fсопротив/m = a
3000 - 500/1000 = a
a = 2,5 м/с²