при такой конфигурации может быть значительно больше силы с которой на сетку действует мяч. Чем туже натянута будет сетка, тем ближе α к 180°, а α/2 к 90° (косинус в знаменателе стремится к нулю). Соответственно, тем больше натяжение сетки будет превосходить силу удара мяча. И возможно будет превышен предел прочности сетки.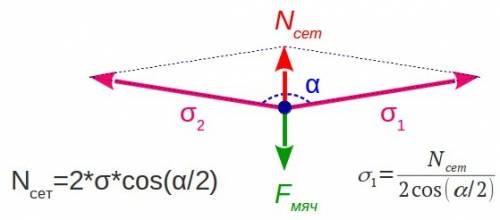 
1) Найди два ближайших штриха шкалы (около которых написаны числовые значения).
2) Потом из большего значения вычитай меньшее.
3) Полученное число раздели на число делений, находящихся между этими двумя ближайшими штрихами.