Вам даны кастрюля на 5литров ведро с водой на 8литров и чайник на 3 литра нужно отмерить наиболее точнее 2,5 л

👇

Увидеть ответ

Ответ:

Mariyaftolov

30.09.2020

Вылеваем в кастрюлю. Остаётся 3 литра. Выливаем в чайник на глаз 2 литра. А затем половину из ведра. Вот и 2,5 литра

4,4(71 оценок)

Открыть все ответы

Ответ:

vadimkakuz200

30.09.2020

Задать во Войти

АнонимФизика31 января 18:37

В горелке сжигается топливо массой m1. КПД горелки n. Полезная теплота Q передается куску меди, массой m2. В результате

чего его температура T повышается от T1 до T2. Нагретую медь кладут на большую льдину при T=273 К. Масса образовавшейся воды m3. дано: дерево m1 = 349г m2 = 8 кг T1 = 285К m3 = 1,16кг Найти: n Q T2

ответ или решение

Данные: m1 (масса сгоревшего топлива (сухих дров)) = 349 г = 0,349 кг; m2 (масса куска меди) = 8 кг; Т1 (исходная температура куска меди) = 285 К; m3 (масса образовавшейся воды) = 1,16 кг; T (первоначальная температура льдины) = 273 К.

Постоянные: qд (уд. теплота сгорания сухих дров) = 107 Дж/кг; См (уд. теплоемкость меди) = 400 Дж/(кг*К); λ (уд. теплота плавления льда) = 34 * 104 Дж/кг.

1) Теплота, полученная большой льдиной от куска меди (полезная теплота): Q = λ * m3 = 34 * 104 * 1,16 = 39,44 * 104 Дж = 394,4 кДж.

2) Конечная температура куска меди: T2 = Q / (Cм * m2) + Т = Q / (Cм * m2) + Т = 39,44 * 104 / (400 * 8) + 273 = 396,25 К.

3) КПД горелки: η = Q / Qд = Q / (qд * m1) = 39,44 * 104 / (107 * 0,349) = 0,113 или 11,3%.

4,5(24 оценок)

Ответ:

mmmm0

30.09.2020

1) Заметим, что какая бы ни была цепочка, если сопротивления всех ее звеньев увеличить вдвое, ее эквивалентное сопротивление также возрастет вдвое.

Заметим что наша цепочка это резистор r, резистор r и паралелльно к нему присоединенная такая же бесконечная цепочка, но с удвоенным сопротивлением, и еще резистор r

Поэтому

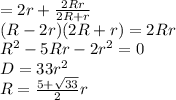
$\displaystyleR = 2r + \frac{2Rr}{2R+r}\\(R-2r)(2R+r) = 2Rr\\R^2-5Rr-2r^2 = 0\\D = 33r^2\\R = \frac{5+\sqrt{33}}{2}r$

2) Обозначим ток, ушедший в первый горизонтальный резистор как A1, а ток ушедший в первый вертикальный резистор как B1, во второй горизонтальный A2, во второй вертикальный B2 и т д. Для любого звена с номером n имеем два правила Кирхгофа

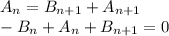
$A_n = B_{n+1}+A_{n+1}\\-B_n + A_n + B_{n+1}=0$

Отсюда

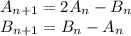
$A_{n+1} = 2A_n - B_n\\B_{n+1} = B_n-A_n$

Пусть полный ток I в первом звене разделился как

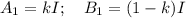
$A_1 = kI;\quad B_1 =(1-k)I$

Посчитаем несколько первых звеньев по полученному правилу

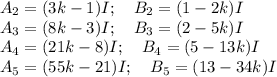
$A_2 = (3k-1)I;\quad B_2 = (1-2k)I\\A_3 = (8k-3)I;\quad B_3 = (2-5k)I\\A_4 = (21k-8)I;\quad B_4 = (5-13k)I\\A_5 = (55k-21)I;\quad B_5 = (13-34k)I$

Заметим что коэффициенты при k в скобках и свободные члены это все числа Фибоначчи! Причем множитель при k это число Фибоначчи с номером на 2 большим, чем соответствующий свободный член.

При стремлении n к бесконечности, отношение коэффициента при k и свободного члена стремится (как отношение двух чисел Фибоначчи с номерами n и n+2) к Ф^2, где число Ф = (1+√5)/2 - золотое сечение. Если k не будет равен 1/Ф^2, мы получим в итоге неограниченный рост токов при стремлении n к бесконечности, чего не может быть. Для компенсации растущих чисел Фибоначчи мы понимаем что k может быть только равен 1/Ф^2.

Теперь вспомним про два крайних резистора и посчитаем перепад напряжения от A к B идя по самому нижнему контуру (по последнему вертикальному резистору течет нулевой ток)

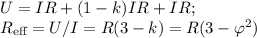
$U = IR + (1-k)IR + IR;\\R_\text{eff} = U/I = R(3-k) = R(3-\varphi^2)$