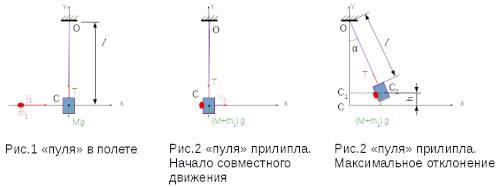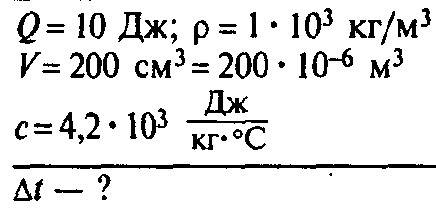
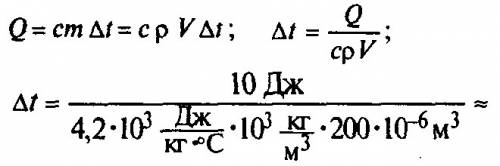
Самое простое из всех неравномерных движений — это прямолинейное движение с постоянным ускорением.
При движении с постоянным ускорением (a→=const−→−−) скорость тела линейно зависит от времени:
v→=v→o+a→t.
В проекциях на ось Ox данные равенства имеют вид:
ax=const;
vx=vox+axt.
Построим графики зависимостей ax(t) и vx(t) для случаев ax>0 и ax<0.
Примем vox>0.
Поскольку в обоих случаях ax=const, то графиком зависимости ax(t) ускорения от времени в обоих случаях будет прямая, параллельная оси времени.
Только при ax>0 данная прямая будет лежать в верхней полуплоскости (рис. 1), а при ax<0 — в нижней (рис. 2).

Рис. 1

Рис. 2
Графиком зависимости скорости движения тела от времени vx(t) является прямая, пересекающая ось скорости в точке
 (1)
(1)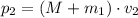 (2)
(2)
 (3)
(3) (4)
(4)
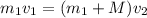
 (5)
(5)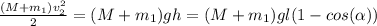
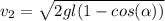 (6)
(6) (7)
(7)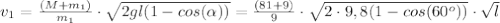
 м/с
м/с