Архимед служил царю, к которому принести корону. Царь хотел знать, есть ли в короне примеси серебра, поэтому и позвал ученого. Архимед долго размышлял, ничего не придумал и однажды решил сходить в баню. Там Архимед обратил внимание на совершенно очевидную вещь: тело, погружаясь в воду, вытесняет объем воды, равный собственному объему тела. Явившись к царю, Архимед попросил выдать ему слитки серебра и золота, равные по массе короне. Измеряя и сравнивая объем воды, вытясняемой короной и слитками, Архимед обнаружил, что корона изготовлена не из чистого золота, а имеет примеси серебра

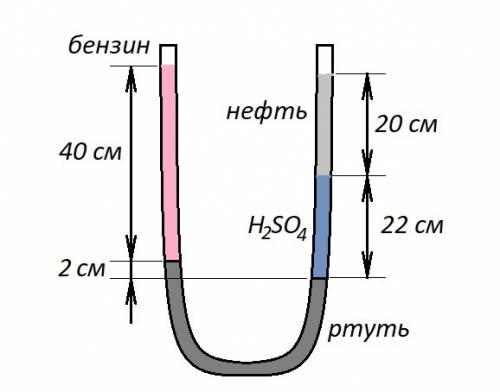
1-ртуть
2-бензин
3-серная кислота
4-нефть
давление в левом колене равно давлению в правом колене
Pл =Pпр
P1+P2 = P3+P4
ρ- плотность жидкости
g-ускорение св.падения
h-высота столба жидкости
ρ1 g h1 + ρ2 g h2 = ρ3 g h3 + ρ4 g h4
ρ1 h1 + ρ2 h2 = ρ3 h3 + ρ4 h4
ρ3 h3 = ρ1 h1 + ρ2 h2 - ρ4 h4
ρ3 = (ρ1 h1 + ρ2 h2 - ρ4 h4) /h3
ρ1 = 13,6 г/см3; h1 = 2 см
ρ2 = 0,7 г/см3; h2 = 40 см
ρ3 = ? ; h3 = 22 см
ρ4 = 0,8 г/см3; h4 = 20 см
ρ3 = (13,6 * 2 + 0,7 * 40 - 0,8 * 20) / 22 = 1,8 г/см3;
ответ
ρ3 = 1,8 г/см3;
пусть а-количество золотых монет на 1 чаше. в-кол. серебр. монет на 1чаше. с-кол. золотых монет на 2 чаше. d-кол. серебр. монет на 2 чаше.
получим систему
1) 19аV+10вV=19cV+10dV+1
2) 19(a+2)V+10(в-5)V+2=19(с-2)V+10(d+5)V
из которой выражаем объем
V=1/(19(a-c)+10(в-d)) из первого уравнения
V=2/(19(c-a-4)+10(d-в-4)+24) из второго уравнения
приравнивая получим 1,5(19(a-c)+10(в-d))=12
тогда по первому уравнению V=1/8=0,125 см3