![F-\mu mg*cos \alpha -mg* sin \alpha =0 \\ F=\mu mg*cos \alpha + mg*sin \alpha \\ F=mg(\mu cos \alpha +sin \alpha )\[[1]](/tpl/images/0280/3532/20b34.png)
![A_3=mgl(\mu cos \alpha +sin \alpha )\[[2]](/tpl/images/0280/3532/51016.png)
![A=mgl*sin \alpha [3]](/tpl/images/0280/3532/07049.png)
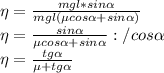
![\eta=\frac{tg \alpha }{\mu+tg \alpha }\\ \frac{1}{\eta}=\frac{\mu+tg \alpha }{tg \alpha }\\ \frac{1}{\eta}=\frac{\mu \alpha }{tg \alpha }+1\\ \eta=\frac{tg \alpha }{\mu \alpha }+1 \ [4]](/tpl/images/0280/3532/7ceb1.png)
![F=mg(\mu cos \alpha +sin \alpha )\\ F=mg\mu cos \alpha +mgsin \alpha\\ mg\mu cos \alpha=F-mgsin \alpha\\ \mu=\frac{F-mgsin \alpha}{mg cos \alpha}\\ \mu=\frac{F}{mg cos \alpha}-tg \alpha\ [5]](/tpl/images/0280/3532/fb858.png)
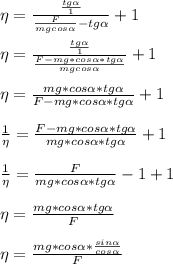
![ \eta= \frac{mg*sin \alpha }{F}\ [5] \\\\](/tpl/images/0280/3532/99c09.png)
осциллятор, представляющий собой механическую систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся в однородном поле сил тяготения[1]. Другой конец нити (стержня) обычно неподвижен. Период малых собственных колебаний маятника длины L, подвешенного в поле тяжести, равен
{\displaystyle T=2\pi {\sqrt {L \over g}}}T=2\pi {\sqrt {L \over g}}
и не зависит, в первом приближении, от амплитуды колебаний и массы маятника. Здесь g — ускорение свободного падения.
Математический маятник служит простейшей моделью физического тела, совершающего колебания: она не учитывает распределение массы. Однако реальный физический маятник при малых амплитудах колеблется так же, как математический с приведённой длиной.
Объяснение:
v1= 40 км/ч
v2= 65 км/ч
l=1 км
t-?
СИ
40×1000/3600=11,11 м/с (На целое число не делится)
65×1000/3600=18,05 м/с ( На целое число не делится)
1×1000=1000 м
Решение;
Поезда едят в одну сторону =>
v=v2-v1 (Если рассматривать скорость относительно первого поезда)
v=18,05-11,11
v=6,94 м/с
t=s/v
t=1000/6,94=144 с
Если без СИ
v=v2-v1. (Если рассматривать скорость относительно первого поезда)
v=65-40=25 км/ч
t=s/v
t=1/25
t=0,04 часа