Интересная задача
Дано:
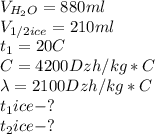
Для начала вспомним закон сохранения мас. Масса неизменная при переходе телом из одного агрегатного состояния в другое.
Поэтому мы может высчитать масу снега в термосе.
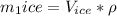
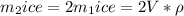
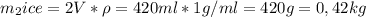
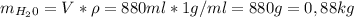
Мы нашли масу снега, поэтому подставим в уравнение теплового баланса
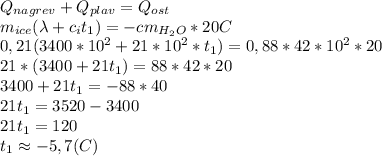
Минус появился, поскольку мы решали только арифметику, и не учитывали, кто теплоту отдает.
Второй вопрос можно решить логически. По сути у нас удельная теплоемкость льда в два раза меньше, а массу при этом мы берем вдвое больше, поэтому можно будет поделить обе части на эту теплоемкость и получится:
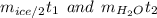
Очевидно, что масса снега меньше, чем воды (примерно в 4 раза), если подставить температуру 20 в правую часть, то при сравнении будет знак <, то бишь у воды еще останется запас теплоты.
Но на плавление льда её не хватит, поскольку лямбда намного больше чем. 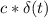
Интересная задача
Дано:
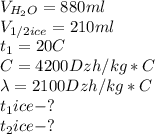
Для начала вспомним закон сохранения мас. Масса неизменная при переходе телом из одного агрегатного состояния в другое.
Поэтому мы может высчитать масу снега в термосе.
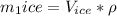
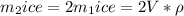
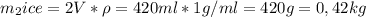
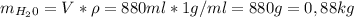
Мы нашли масу снега, поэтому подставим в уравнение теплового баланса
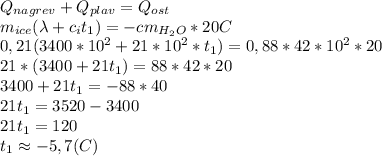
Минус появился, поскольку мы решали только арифметику, и не учитывали, кто теплоту отдает.
Второй вопрос можно решить логически. По сути у нас удельная теплоемкость льда в два раза меньше, а массу при этом мы берем вдвое больше, поэтому можно будет поделить обе части на эту теплоемкость и получится:
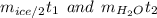
Очевидно, что масса снега меньше, чем воды (примерно в 4 раза), если подставить температуру 20 в правую часть, то при сравнении будет знак <, то бишь у воды еще останется запас теплоты.
Но на плавление льда её не хватит, поскольку лямбда намного больше чем. 
λ₁ = 23 000 Дж на кг - удельная теплота плавления свинца
ΔT₁ = 327 - 27 = 300 C снижение температуры свинца
С₁ = 130 Дж на кг на град - удельная теплоёмкость свинца
Тепло, выделившееся при отвердевании и остывании свинца
Q₁ = m₁(λ₁ + С₁ΔT₁)
m₂ = 100 г = 0.1 кг - масса льда
С₂ = 2100 Дж на кг на град - удельная теплоёмкость льда
С₃ = 4200 Дж на кг на град - удельная теплоёмкость воды
λ₂ = 330 000 Дж на кг - удельная теплота плавления льда
ΔT₂ = 0 - (-10) = 10 С - нагрев льда до температуры плавления
ΔT₃ = 27 - 0 = 27 С - нагрев воды до равновесной температуры
ΔT₄ = 100 - 0 = 100 С - нагрев воды до точки кипения
λ₃ = 2 256 000 Дж на кг - удельная теплота испарения воды
x - доля выкипевшей воды
Тепло, поглощенное при нагреве и расплаве льда а также при нагреве талой воды частью до равновесной температуры, частью - до температуры кипения плюс тепло, затраченное на выкипание части воды равно:
Q₂ = m₂(λ₂ + C₂ΔT₂ + C₃(1-x)ΔT₃ + C₃xΔT₄ + xλ₃)
Уравнение баланса получается из условия Q₁ = Q₂
m₁(λ₁ + С₁ΔT₁) = m₂(λ₂ + C₂ΔT₂ + C₃(1-x)ΔT₃ + C₃xΔT₄ + xλ₃)
Выделив xm₂ из этого уравнения, получим:
xm₂ = (m₁(λ₁ + С₁ΔT₁) - m₂(λ₂ + C₂ΔT₂ + C₃ΔT₃))/(λ₃ + C₃(ΔT₄ - ΔT₃))
xm₂ = (1.5*(23 000 + 130*300) - 0.1*(330 000 + 2100*10 + 4200*27)/(2 256 000 + 4200*(100 - 27)) = (93 000 - 46 440)/2 562 600 = 0.018 кг
Из 100 граммов льда при начальной температуре -10 С выкипело 18 граммов воды при отвердевании свинца, налитого при температуре плавления и остывании его (свинца) до 27 градусов.