Заменим силу натяжения двух тросов на равнодействующую.
Здесь можно принять за аналогию треугольную пирамиду.
Проведём сечение через один из тросов с углом 12 градусов.
Равнодействующая будет равна двум апофемам.
Тангенс угла α наклона апофемы в 2 раза больше тангенса угла наклона троса.
tg α = 2*tg 12° = 2*0,212556562 = 0,425113123,
α = arc tg = 0,425113123 = 23,03098167 градуса.
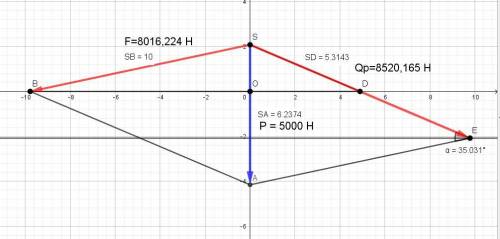
Во вложении дана схема, на которой видно, то усилие в тросе соответствует гипотенузе прямоугольного треугольника, катетом которого есть третья часть вертикальной нагрузки.
P = (1/3)*500*10 = (5000/3) H.
F = (5000/3) / sin12° = 8016,224 H.
сопротивление стало больше, количество теплоты стало меньше.
Объяснение:
Вопросы какие-то... странные.
Ну, ладно.
У "обычного" провода есть какое-то сопротивление R, на котором при протекании через него тока I выделяется по закону Джоуля-Ленца количество теплоты
Q=P*t, где
P - мощность электрического тока в сопротивлении (проводе), Вт
t - единица времени, в течение которой считаем количество теплоты, с.
Причем
P=I²*R или (вспомнив закон Ома) P=U²/R
Получаем:
Q=U²*t/R [Дж]
Добавив к "обычному" проводу кусок медного последовательно (т.е. удлиннив "обычный") мы увеличим общее сопротивление провода на величину сопротивления медного куска Rм. Вобщем-то увеличение произойде при любом материале провода (и при серебре, и при дереве). Получим новое сопротивление:
R'=R+Rм; R'>R
Q'=U²*t/R';
т.к. знаменатель стал больше, то число стало меньше (при условии, что величина напряжения не изменяется):
Q'<Q
R=190 м F=Gm₁m₂/R²=Gm²/R²;
G=6,67 10¹¹ Н м²/кг² F=6,67 10⁻¹¹*78000*78000/190*190=
=6,67 10⁻¹¹6,084 10⁻⁹/3,61 10⁻⁴=11,24 10⁻¹⁶ H
F-? ответ: F=11,24 10⁻¹¹ H.