Объяснение:
Дано:
U=270 B
R2 = 12 Ом
R4 = 22 Ом
R5 = 16 Ом
R6 = 10 Ом
L2 = 14 мГн
L3 = 8 мГн
C1 = 11 мкФ
C3 = 22 мкФ
ν = 50 Гц
_________
1)
Находим активное сопротивление цепи:
R = R2+R4+R5+R6 = 12+22+16+10 = 60 Ом
2)
Находим реактивные сопротивления катушек:
XL = XL2+XL3 = 2π*ν*L2+2π*ν+L3 = 2π*ν*(L2+L3)=
=2*3,14*50*(14+8)*10⁻³ ≈ 69 Ом
3)
Находим реактивное сопротивление емкостей:
Xc = Xc1+Xc3 = 1 / (2π*ν*C1) + 1/(2π*ν*C3) = 1/(2π*ν)*(1/C1+1/C3) =
= 1/(2*3,14*50) * (1/11*10⁻⁶+1/22*10⁻6) ≈ 1/(2*3,14*50)*(1/11e-6+1/22e-6)≈434 Ом
4)
Находим общее сопротивление цепи:
Z = √ (R²+ (Xc-XL)²) = √ (60² + (434-69)²) ≈ 670 Ом
5)
Находим общий ток:
I = U / Z = 270 / 670 ≈ 0,4 А
6)
Находим активную мощность:
P =I²*R = 0,4²*60 = 9,6 Вт
7)
Ну а теперь последовательно находим напряжения на элементах цепи:
Резисторы:
U2 = I*R2 = 0,4*12 = 4,8 B
U4 = I*R4 = 0,4*22 = 8,8 B
U5 = I*R5 = 0,4*16 = 6,4 B
U6 = I*R6 = 0,4*10 = 4,0 B
На катушках:
UXL2 = 2*π*ν*L2*I = 2*3,14*50*14*10⁻³ *0,4 ≈ 1,8 B
Аналогично на XL3 (рассчитать самостоятельно!)
Напряжение на конденсаторах:
UXc1 = I*(1/(2π*ν*C) = 0,4*1/(2*3,14*50*11*10⁻⁶) ≈ 116 В
(Аналогично на другом конденсаторе рассчитать самостоятельно)
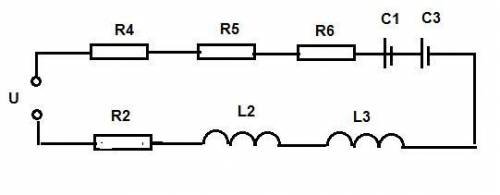
Электрическая схема:
Бо́ровская моде́ль а́тома (Моде́ль Бо́ра) — полуклассическая модель атома, предложенная Нильсом Бором в 1913 г. За основу он взял планетарную модель атома, выдвинутую Резерфордом. Однако, с точки зрения классической электродинамики, электрон в модели Резерфорда, двигаясь вокруг ядра, должен был бы излучать энергию непрерывно и очень быстро и, потеряв её, упасть на ядро. Чтобы преодолеть эту проблему, Бор ввёл допущение, суть которого заключается в том, что электроны в атоме могут двигаться только по определённым (стационарным) орбитам, находясь на которых они не излучают энергию, а излучение или поглощение происходит только в момент перехода с одной орбиты на другую. Причём, стационарными являются лишь те орбиты, при движении по которым момент количества движения электрона равен целому числу постоянных Планка[1]: {\displaystyle m_{e}vr=n\hbar \ } m_{e}vr=n\hbar \ .
Используя это допущение и законы классической механики, а именно равенство силы притяжения электрона со стороны ядра и центробежной силы, действующей на вращающийся электрон, он получил следующие значения для радиуса стационарной орбиты {\displaystyle R_{n}} R_n и энергии {\displaystyle E_{n}} E_{n} находящегося на этой орбите электрона:
{\displaystyle R_{n}=4\pi {\frac {\varepsilon _{0}}{Ze^{2}}}{\frac {n^{2}\hbar ^{2}}{m_{e}}};\quad E_{n}=-{\frac {1}{8\pi }}{\frac {Ze^{2}}{\varepsilon _{0}}}{\frac {1}{R_{n}}};} {\displaystyle R_{n}=4\pi {\frac {\varepsilon _{0}}{Ze^{2}}}{\frac {n^{2}\hbar ^{2}}{m_{e}}};\quad E_{n}=-{\frac {1}{8\pi }}{\frac {Ze^{2}}{\varepsilon _{0}}}{\frac {1}{R_{n}}};}
Здесь {\displaystyle m_{e}} m_e — масса электрона, {\displaystyle Z} Z — количество протонов в ядре, {\displaystyle \varepsilon _{0}} \varepsilon _{0} — электрическая постоянная, {\displaystyle e} e — заряд электрона.
Именно такое выражение для энергии можно получить, применяя уравнение Шрёдингера в задаче о движении электрона в центральном кулоновском поле.
Радиус первой орбиты в атоме водорода R0=5,2917720859(36)⋅10−11 м[2], ныне называется боровским радиусом, либо атомной единицей длины и широко используется в современной физике. Энергия первой орбиты {\displaystyle E_{0}=-13.6} E_{0}=-13.6 эВ представляет собой энергию ионизации атома водорода.