Дуга окружности с центром в точке касания диска с поверхностью и радиусом, равным радиусу диска
Объяснение:
Если диск катится без проскальзывания, то его мгновенным центром скоростей является точка соприкосновения с поверхностью. Скорость любой точки на диске может быть рассчитана из выражения:
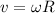
где ω - угловая скорость вращения диска относительно мгновенного центра скоростей
R - расстояние от рассматриваемой точки до мгновенного центра скоростей.
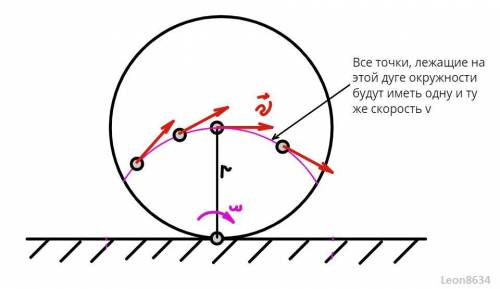
Из рисунка видно, что геометрическим местом точек, имеющих скорость v является дуга окружности с центром в точке касания диска с поверхностью и радиусом, равным радиусу диска.
1) Сначало найдём силу тока,протекаемую в цепи по закону Ома:
I = U2/R2 = 12/6 = 2 (A)
2)На R3 выделится теплота
Q = I^2 * R3 * t = 2,4 ( КДж)
Находим R3 = 2.4*10^3/2^2*60 = 10 (Ом)
ответ: 10 Ом