Пояснение к рисункам:
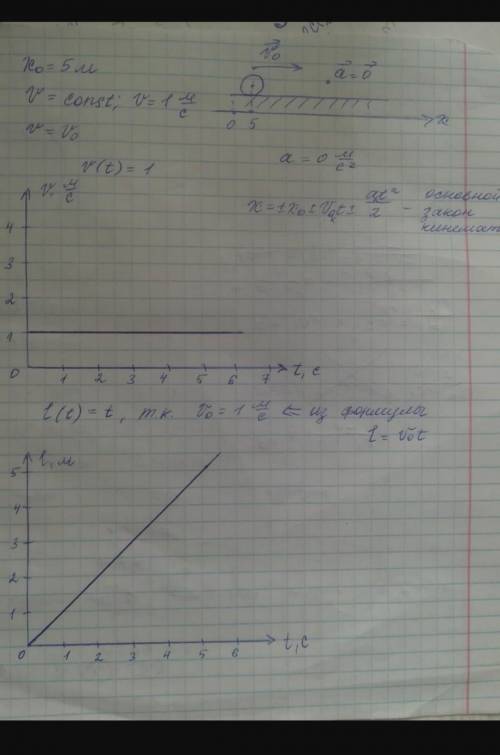
Нарисуем физический рисунок и обозначим на нем известные величины. В условии сказано, что тело движется со скоростью 1 м/с, т. е. скорость тела не изменяется, значит, V=const, V0=V. Тело движется вдоль оси ОХ, и движется сонаправленно. Начальная координата тела - 5 м, я спроецировала её на ось ОХ. Делаем вывод о том, что движение равномерное и прямолинейное.
При прямолинейном движении ускорение равно 0 м/с^2.
Основной закон кинематики:
x=±x0±V0x*t±axt^2/2
Воспользуемся им.
1. V(t). Скорость при прямолинейном равномерном движении, как было сказано ранее, константа, поэтому график имеет вид прямой и параллелен оси Оt.
2. l(t). Из основного закона кинематики: S=V0t+at^2/2, а в данном случае S=l.
Из формулы l=V0t (а=0 м/с^2, поэтому опускаем второе слагаемое) после подстановки значения V0 (а это у нас 1 м/с) имеем функцию l=1t.
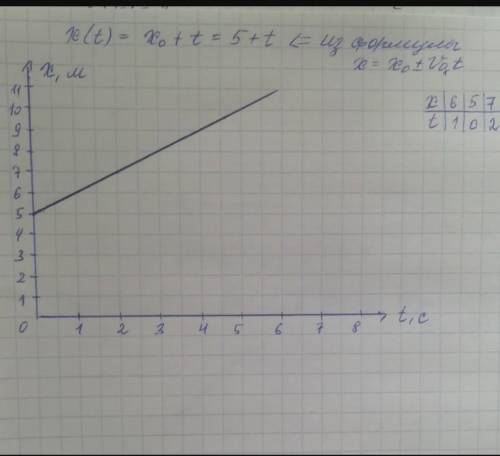
3. x(t). Пользуемся основным законом кинематики, подставляем известные значения x0, V0 и получаем функцию вида x=5+t.
Объяснение:
ответ:Чтобы вычислить значение КПД указанной наклонной плоскости, воспользуемся формулой: η = Апол / Азатр = m * g * h / (F * l).
Постоянные и переменные: m — масса вытаскиваемого груза (m = 100 кг); — ускорение свободного падения (g ≈ 10 м/с2); h — высота вытаскивания груза (h = 2 м); F — приложенная сила (F = 800 Н); l — длина указанной наклонной плоскости (l = 4 м).
Вычисление: η = m * g * h / (F * l) = 100 * 10 * 2 / (800 * 4) = 0,625 (62,5%).
ответ: КПД указанной наклонной плоскости равен 62,5%.
Объяснение: