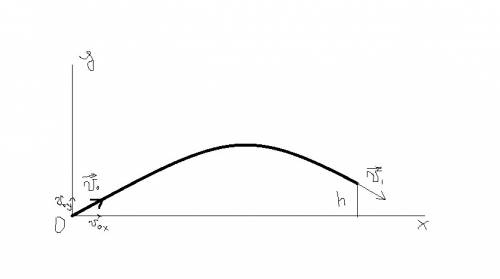
Введем систему координат с началом в точке отправления мяча (см. рисунок).
Запишем законы движения по осям:
(1) 
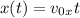
(2) 
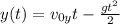
По условию известна скорость в точке 1, где y=h.
Найдем время полета мяча до кольца:
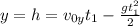
Имеем квадратное уравнение относительно t, его решения:
.
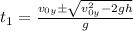Скорость мяча найдем, дифференцируя уравнения (1) и (2):
(3) 
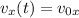
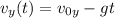, подставим сюда выражение для времени полета, получим:
(4) 
.
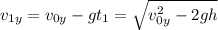По теореме Пифагора:
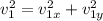, подставим сюда выражение (3) и (4):
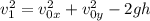
Отсюда, окончательно имеем:
.
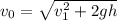Подставим сюда значения из условия:
v₀ = √(9 + 2*9.8*1) = 5.3 м/с
Для этого надо знать плотность луны или ее массу, а также расстояние от земли до луны и радиус земли.
L(расстояние)=385000км=385000000м
Rземли=6400км=6400000м
F=MmG/R^2
F=ma, если человек стоит на земле, то ускорение свободного падения равно g=>Fт=mg=MmG/R^2=>gR^2=MG Пусть MG=const X
Для притяжения к земле с луны верно равенство
gприт(новое притяжение)*(R+L)^2=X
Дальше выразим gприт=gR^2/(R+L)^2
Fтяж к земле=(gR^2/(R+L)^2)m
Fтяж к луне=GmM/r^2
Fлун/Fзем=gR^2/(R+L)^2 /GM/r^2=gR^2*r^2/(R+L)^2*GM
Подставь величины=)))
Удачи
ЭДС=I1(R1+r)=I2(R2+r)
I1R1+I1r=I2R2+I2r
r(I1-I2)=I2R2-I1R1
r=(I2R2-I1R1)/(I1-I2)
Из закона Ома:
U2=I2*R2
U1=I1*R1
r=(U2-U1)/(I1-I2)=(2-2,1)B/(2-4)A=0,05Ом
ответ: 0,05 Ом