Объяснение:
Подумайте, почему лунное затмение мы наблюдаем чаще, чем солнечный, ведь за год их количество почти одинакова
Ну это как сказать почти одинаково...
В среднем солнечные затмения случаются в 1,5 раз чаще чем лунные , но человек за свою жизнь ( живущий хотя бы приблизительно на одном месте ) видит всё же чаще лунные затмения чем солнечные а вот почему
Когда случается солнечное затмение его видно на Земле в довольно узком диапазоне ( согласно данным цитата : "Ширина тени Луны на Земной поверхности не превышает 270 км" ) , что делает и вправду это явление довольно редким нежели чем лунное затмение ведь когда происходит лунное затмение его видно с половины Земли!
В общем-то к ответу для наглядности прикреплю схематичные рисунки
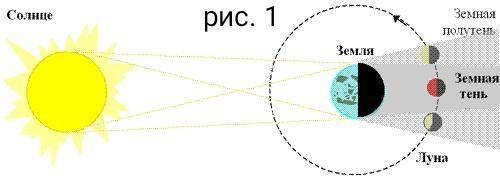
Рис. 1 - лунное затмение
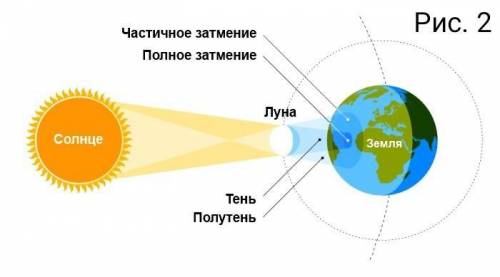
Рис. 2 - солнечное затмение
( Объекты на рисунках конечно же не соответствуют реальным размерам Солнца , Земли и Луны но они сделаны лишь для наглядности происходящего! )
x-компонента импульса летящей пули: Px = m v cos(a)
x-компонента импульса катящегося бруска с пулей внутри:
Px = (m+M) Uo
m v cos(a) = (m+M) Uo
Uo = [ m cos(a) / (m + M) ] v - знаем начальную скорость бруска
дальше для движения бруска запишем второй закон Ньютона:
(m+M) a = - k (m + M) g
a = k g - модуль ускорение бруска
x(t) = Uo t - a t^2 / 2 - величина смещения бруска в зависимости от времени
u(t) = Uo - a t - скорость бруска, в зависимости от времени
Найдем момент, когда скорость уменьшилась на 20%:
u(to) = Uo - a to = 0,8 Uo
0,2 Uo = a to
to = 0,2 Uo / a
Пройденный путь за это время:
X(to) = Uo t - a t^2 / 2 = (0,18/a) Uo^2
Подставим Uo и a:
X(to) = (0,18/k) [m cos(a) / (m+M)]^2 (v^2 / g) = 9,2(см)