Question

Свысотой 9,62 м бросили мячик вертикально вверх с начальной скоростью 5м/с. определите время полетаи скорость тела в момент удара о землю

Answer 1

По условию:

h₀ = 9,62 м;

V₀ = 5 м/с.

t, V - ?

Решение:

В данной задаче следует рассматривать три момента:

1) Момент броска мяча, V₀ = 5 м/с, h₀ = 9,62 м.

2) Момент, когда мяч достигает верхней точки, V' = 0 м/c,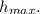 $h_{max}.$

3) Момент приземления, h = 0 м, t - ?

Время полёта поделим на 2 части: время от момента (1) до момента (2) (пусть t₁) и далее от момента (2) до (3) (пусть t₂). Значит, t = t₁ + t₂.

Время t₁ определим из уравнения зависимости скорости от времени:

$V' = V_0 - gt_1,$

$t_1 = \frac{V_0 - V'}{g} = \frac{5-0}{10} = 0,5$ (c).

Перед нахождением времени t₂ нужно найти максимальную высоту, на которой мячик остановится, перед тем как начать падать. Для этого воспользуемся уравнением движения:

$h_{max} = h_0 + V_0t_1 - \frac{gt_1^2}{2} = 9,62 + 5*0,5 - \frac{10*0,5^2}{2} = 10,87$ (м).

С текущими данными мы сможем найти скорость перед приземлением, используя следующую формулу и учитывая, что V' = 0:

$h_{max} = \frac{V^2 - V'^2}{2g} = \frac{V^2}{2g},$

$V = \sqrt{2gh_{max}} = \sqrt{2*10*10,87} = 14,74$ (м/с).

Теперь, зная максимальную высоту, найдём время t₂ через уравнение движения:

$h = h_{max} - \frac{gt_2^2}{2} = 0,$

$t = \sqrt{\frac{2h_{max}}{g}} = \sqrt{\frac{2*10,87}{10}} = 1,47$ (c).

Таким образом, t = 0,5 + 1,47 = 1,97 (c).

ответ: 1,97 с; 14,74 м/с.