солютный показатель преломления вещества — величина, равная отношению фазовых скоростей света (электромагнитных волн) в вакууме и в данной среде n=c/v
Величина n, входящая в закон преломления, называется относительным показателем преломления для пары сред.
Величина n есть относительный показатель преломления среды В по отношению к среде А, а n' = 1/n есть относительный показатель преломления среды А по отношению к среде В.
Эта величина при прочих равных условиях больше единицы при переходе луча из среды более плотной в среду менее плотную, и меньше единицы при переходе луча из среды менее плотной в среду более плотную (например, из газа или из вакуума в жидкость или твердое тело). Есть исключения из этого правила, и потому принято называть среду оптически более или менее плотной, чем другая.
Луч, падающий из безвоздушного пространства на поверхность какой-нибудь среды В, преломляется сильнее, чем при падении на нее из другой среды А; показатель преломления луча, падающего на среду из безвоздушного пространства, называется его абсолютным показателем преломления .
p = n*k*T => n = p/(k*T) - концентрация молекул, число молекул в 1 м³
V₀ = 1 / n, где V₀ - объем пространства занимаемый одной молекулой
V₀ = k * T / p = 1,38*10⁻²³ Дж/К * 273 К / 10⁵ Па ≈ 3,77*10⁻²⁶ м³
Этот объем равен объему сферы диаметра D равного среднему расстоянию между молекулами r
π * D³ / 6 = π * r³ / 6 = V₀ => r = ∛(6 * V₀ / π)
r = ∛(6 * 3,77*10⁻²⁶ м³ / 3,14) ≈ 4,2*10⁻⁹ м
v₀ - объем одной молекулы => v₀ = π * d₀³ / 6, d₀ - диаметр молекулы
N = 1 м³ * n - число молекул в 1 м³
∑v₀ = 1 м³ * n * v₀ = 1 м³ * p * π * d₀³ / (6 * k * T) - суммарный объем всех молекул в 1 м³
1 м³ / ∑v₀ = 6 * k * T * 1 м³ / (π * p * d₀³ * 1 м³) = 6 * k * T / (π * p * d₀³)
1 м³ / ∑v₀ = 6 * 1,38*10⁻²³ Дж/К * 273 К / (3,14 * 10⁵ Па * (3*10⁻¹⁰ м)³) ≈ 2,7*10³ = 2700 раз
Длина нити: L = 5 м.
Масса: m = 5 кг.
Время: t = 2 мин = 120 с.
Найти нужно число колебаний: N - ?
Решение:1. Формула периода математического маятника: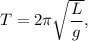
где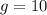
м/с² - ускорение свободного падения.
2. Общая формула периода: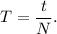
3. Объединяем (1) и (2):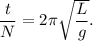
4. Выразим количество колебаний из (3):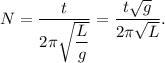
Численно получим: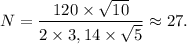
ответ: 27 колебаний.