Решение на фото. Расплавилась только 1/8 всей пули.
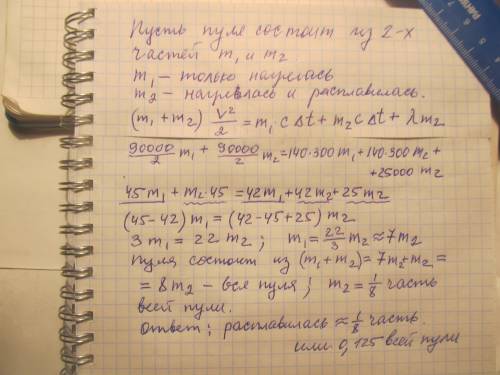
1. Второй положительный заряд надо расположить за отрицательным зарядом на расстоянии 10 см. Придется исследовать равновесие только одного из положительных зарядов. Отрицательный будет в равновесии. Для экономии времени не буду писать полностью коэффициент. k*(q*q1))/(r^2)=k*(q^2)/((r+x)^2) ;
q1/q=(r^2)/((r+x)^2); r/(r+x)=(q1/q)^0,5; 10/(10+x)=(10/40)^0,5; 2*10=10+x; x=10. Второй положительный заряд надо расположить на расстоянии 10 см от отрицательного заряда и на расстоянии 20 см от положительного заряда чем смогла.
1. Второй положительный заряд надо расположить за отрицательным зарядом на расстоянии 10 см. Придется исследовать равновесие только одного из положительных зарядов. Отрицательный будет в равновесии. Для экономии времени не буду писать полностью коэффициент. k*(q*q1))/(r^2)=k*(q^2)/((r+x)^2) ;
q1/q=(r^2)/((r+x)^2); r/(r+x)=(q1/q)^0,5; 10/(10+x)=(10/40)^0,5; 2*10=10+x; x=10. Второй положительный заряд надо расположить на расстоянии 10 см от отрицательного заряда и на расстоянии 20 см от положительного заряда.
Скорость пули: V = 300 м/с.
Начальная температура свинца: t₁ = 27 °C.
Температура плавления свинца: t₂ = 327 °C.
Удельная теплоёмкость свинца: с = 140 Дж/(кг * °С).
Удельная теплота плавления свинца: λ = 25000 Дж/кг.
Обозначим массу всей пули через m₁, а массу расплавленной части пули через m₂.
Найти отношение масс: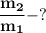
Решение:0. Кинетическая энергия летящей пули переходит в теплоту нагревания свинца и его плавления, то есть: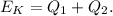
1. Кинетическая энергия летящей пули: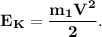
2. Энергия (теплота) нагревания пули: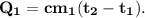
3. Теплота плавления части пули: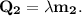
4. Объединяем (0), (1), (2) и (3):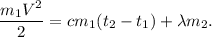
5. Выразим искомое отношение из (4).
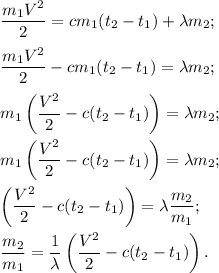
Численно получим: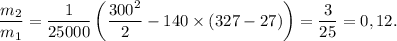
ответ: 0,12 часть.