m1 = 6кг - масса 1-го шара
v1 = 2 м/с - скорость 1-го шара до соударения
m2 = 2 кг - масса 2-го шара
v2 = 0 - скорость 2-го шара до соударения
u - ? - скорость шаров после соударения
До столкновения импульс системы равен m1 · v1 + m2 · v2
После столкновения импульс системы стал m1 · u + m2 · u
Применим теорему сохранения импульса системы:
m1 · v1 + m2 · v2 = m1 · u + m2 · u
u = (m1 · v1 + m2 · v2)/(m1 + m2)
u = (6 · 2 + 2 · 0)/(6 + 2) = 1.5
ответ: скорость шаров после соударения равна u = 1.5 м/с
Найдем формулу, связывающую амплитудное значение тока в контуре с амплитудным значением напряжения. Как известно напряжение в контуре
U(t)=q(t)C=>qmax=Umax∗C(1) В тоже время I(t)=dqdt=q′(t). Величина заряда меняется по гармоническому закону q(t)=qmaxcos(ωt)=>I(t)=q′(t)=−qmax∗ωsin(ωt), таким образом мы получили, что Imax=−qmaxω(2) подставляем (1) в (2) Imax=−UmaxCωОсталось найти циклическую частоту ω=2πT, в то же время период равен по формуле Томсона T=2πLC−−−√, подставляем в (2)Imax=−Umax∗C2πT=−Umax∗C2π2πLC−−−√==−Umax∗CLC−−−√=−UmaxCL−−√Подставляем данные задачи Imax=−500В400∗10−12Ф10∗10−3Гн−−−−−−−−−−−√=−0,1А
Здесь необходимо знать закон сохранения импульса. Начальный импульс будет равен конечному, потому что происходит абсолютно неупругий удар и тела "слипаются"
(формула импульса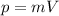 )
)
Начальный импульс: p0=m1*V0
Конечный импульс: p=(m1+m2)*V
p0=p;
m1*V0=(m1+m2)*V;
V=m1*V0/(m1+m2);
Подстановка: V=6*2/(6+2)=12/8=1,5 м/с
ответ: 1,5 м/с