40 ! краткий конспект по атмосферному давлению и измерению атмосферного давления.

👇

Увидеть ответ

Ответ:

yanabutko1999

24.03.2021

а как мы сделаем конспект,если нет самого текста? : ( пришли текст, мы сделаем

4,8(77 оценок)

Ответ:

Anastik222

24.03.2021

атмосферное давление.

атмосфера - слой воздуха, который окружает нашу планету. она представляет собой смесь газов. атмосфера удерживается притяжением земли. на нее действует сила тяжести.

исследования показали, что плотность атмосферы на разных высотах от поверхности земли
различна: она увеличивается по мере приближения к поверхности земли.

если последовательно выделять разные уровни, то можно показать, что каждый вышележащий слой атмосферы вследствие притяжения земли давит на слой, лежащий ниже. но газы, согласно закону паскаля, производимое на них
давление без изменения во все точки. значит, на разных расстояниях от поверхности земли состояние атмосферы можно характеризовать своим давлением. самое большое давление будет наблюдаться вблизи поверхности земли.

атмосфера давит на поверхность земли. это действие называют атмосферным
давлением. атмосферное давление действует на все тела, находящиеся в атмосфере.

впервые установил существование атмосферного давления, изобрел прибор для измерения атмосферного давления и измерил его ученик галилея эванджелиста торричелли.

его опыт состоял в следующем.
узкую трубку длиной 1 м, запаянную с одного конца, торричелли заполнил ртутью. закрыв отверстие пальце, он перевернул ее и погрузил в чашку с ртутью. когда торричелли отпустил палец, часть ртути вылилась из трубки в чашку. высота столбика оставшейся ртути в трубке оказалась равной примерно 76
см.

это явление можно объяснить, если предположить, что давление образовавшегося столба ртути уравновешивает давление атмосферы на уровне свободной поверхности ртути в чашке.

поместив рядом с трубкой шкалу, торричелли наблюдал изменение высоты столба ртути в трубке в связи
с изменениями в атмосфере и измерял атмосферное давление в единицах "высоты ртутного столба". этот прибор называется ртутным барометром. за величину нормального атмосферного давления, измеренного таким способом, принято давление столба ртути высотой 760 мм.

4,8(20 оценок)

Открыть все ответы

Ответ:

mahachik7

24.03.2021

Так как заряженный шар радиуса R смещен от центра сферы на R/2 то любая сфера с центром в заданной точке и радиусом больше R+R/2 содержит внутри исходный заряженный шар с зарядом q
теперь нужно воспользоваться теоремой остроградского-гаусса
поток вектора напряженности электрического поля через замкнутую сферическую поверхность равен заряду ограниченному єтой поверхности делить на Еo
заряд известен, он равен заряду шара, полностью находящегося внутри сферы. Ео - электрическая постоянная
Ф=q/Eo=17,7*10^(-9)/8,85 × 10^-12=2000 В*м

4,7(26 оценок)

Ответ:

Nemsix

24.03.2021

Если пренебречь сопротивлением воздуха и считать снаряд материальной точкой, то задача о движении снаряда, выпущенного из пушки под углом α к горизонту с начальной скоростью v, сводится к известной задаче о движении тела, брошенного под углом к горизонту.
Наложим на систему декартовы координаты, совместив их начало с пушкой и рассмотрим снаряд как материальную точку, участвующую одновременно в двух движениях - по оси х и оси y.
Тогда в некий момент времени t можно записать следующие уравнения для скорости точки:
$\displaystyle v_x=v\cos\alpha \\ v_y=v\sin\alpha-gt$
Уравнение перемещения точки по осям будет иметь вид
$\displaystyle x=vt\cos\alpha \\ y=vt\sin\alpha-\frac{gt^2}{2}$
В любой точке М квадрат расстояния r² от начала координат до этой точки может быть найден по теореме Пифагора. Мы ищем квадрат, чтобы не заморачиваться извлечением квадратного корня, поскольку сама величина r нам не нужна.
$\displaystyle L_M=r_M^2=x_M^2+y_M^2=(vt\cos\alpha)^2+\left(vt\sin\alpha-\frac{gt^2}{2}\right)^2$
Чтобы определить области убывания функции L(t), нужно найти значения t при которых производная L'(t) будет отрицательной.
Упростим L(t), раскрыв скобки и используя основное тригонометрическое тождество, а затем найдем производную.
$\displaystyle L(t)=t^2v^2-vt^3g\sin\alpha+\frac{1}{4}g^2t^4 \\ \frac{dL}{dt}=2tv^2-3vt^2g\sin\alpha+g^2t^3=t(2v^2-3vtg\sin\alpha+g^2t^2)$
Осталось решить неравенство $\displaystyle 2v^2-3vtg\sin\alpha+g^2t^2\ \textless \ 0$
Сначала определим точки, где левая часть обращается в ноль, а потом найдем необходимые интервалы. Получается квадратное уравнение относительно t; его решение тривиально и приводить я его не буду.
Получаем два корня,которые можно записать одним выражением:
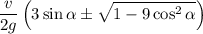
$\displaystyle \frac{v}{2g}\left(3\sin\alpha\pm\sqrt{1-9\cos^2 \alpha}\right)$
Отсюда мы получаем область допустимых значений sin(α) ∈ [2√2/3;1] - значение 1 берем из условия, что углы больше 90° не рассматриваются.
С некоторым приближением можно записать α ∈ [70.53°;90°]
Первый (меньший) корень задает нам точку, начиная с которой расстояние между пушкой и снарядом начинает сокращаться.
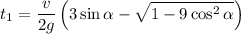
$t_1=\displaystyle \frac{v}{2g}\left(3\sin\alpha-\sqrt{1-9\cos^2 \alpha}\right)$
Второй (больший) корень задает точку, после прохождения которой расстояние снова начинает увеличиваться.
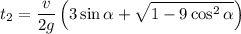
$t_2=\displaystyle \frac{v}{2g}\left(3\sin\alpha+\sqrt{1-9\cos^2 \alpha}\right)$
Но для t₂ необходимо учесть, что наши формулы рассматривают процесс движения тела до бесконечности, а в реальности снаряд может падать ниже уровня пушки лишь разве что в овраг... Поэтому достаточно ограничиться временем движения снаряда при достижении им горизонта пушки, т.е. у=0 в нашей системе координат.
Для этого находим решение уравнения у=0
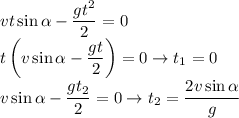
$\displaystyle vt\sin\alpha-\frac{gt^2}{2}=0 \\ t\left(v\sin\alpha-\frac{gt}{2}\right)=0 \to t_1=0 \\ v\sin\alpha-\frac{gt_2}{2}=0 \to t_2= \frac{2v\sin\alpha}{g}$
Тривиальное решение t₁=0 нас не интересует, а вот t₂ - то, что нужно.
Окончательно получаем решение
$\displaystyle t \in \left[t_1;\min\left(t_2,\frac{2v\sin\alpha}{g}\right)\right], \\
t_1=\frac{v}{2g}\left(3\sin\alpha-\sqrt{1-9\cos^2 \alpha}\right) \\ \\
t_2=\frac{v}{2g}\left(3\sin\alpha+\sqrt{1-9\cos^2 \alpha}\right) \\ \\
\alpha \in [70.53^\circ;90^\circ]$
Если интересует длительность промежутка времени, в который приближение происходит, она равна
$\displaystyle \min\left(t_2,\frac{2v\sin\alpha}{g}\right)\right]-t_1$
Если минимум равен t₂, получаем решение
$\displaystyle \frac{v}{2g}\left(3\sin\alpha+\sqrt{1-9\cos^2 \alpha}\right)- \frac{v}{2g}\left(3\sin\alpha-\sqrt{1-9\cos^2 \alpha}\right)= \\ \\ \frac{v}{g}\cdot\sqrt{1-9\cos^2 \alpha}, \ \alpha \in [70.53^\circ;90^\circ]$

Сборник по под редакцией савченко. 1.3.30* звучит так (дословно) снаряд вылетает из пушки со скорост