Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Дано: ΔАВС, ΔА₁В₁С₁,
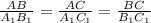
Доказать: ΔАВС подобен ΔА₁В₁С₁.
Доказательство:
На стороне АС треугольника АВС отложим СА₂ = С₁А₁ и проведем А₂В₂║АВ.
Так как прямая, параллельная стороне треугольника, отсекает треугольник, подобный данному, то
ΔАВС подобен ΔА₂В₂С , значит их стороны пропорциональны:
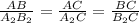 , а так как А₂С = А₁С₁, то получаем
, а так как А₂С = А₁С₁, то получаем
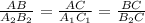 ,
,
По условию:
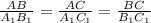 .
.
Из этих двух равенств следует, что
А₂В₂ = А₁В₁ и В₂С = В₁С₁.
Тогда ΔА₁В₁С₁ = ΔА₂В₂С по трем сторонам.
Значит,
ΔАВС подобен ΔА₁В₁С₁.
Объяснение:
1) Против равных углов лежат равные стороны.
Прведем из точки Е прямую ║ стороне СД. (будет точка К)...
Против угла СДЕ лежит сторона СЕ,против равного ему угла ЕДК лежит сторона ЕК=8 см. ЕС=8 см.
Р=2(8+8+2)=36 см.
2)
Задача аналогичная. Против равных углов лежат равные стороны.
Р=2(5+5++5)=30. см.
3)
Δ АКВ равнобедренный,∠К=∠КВА=50°.
∠А=180-50-50=80°.∠А=∠С
∠В=180-80=100°=∠Д.