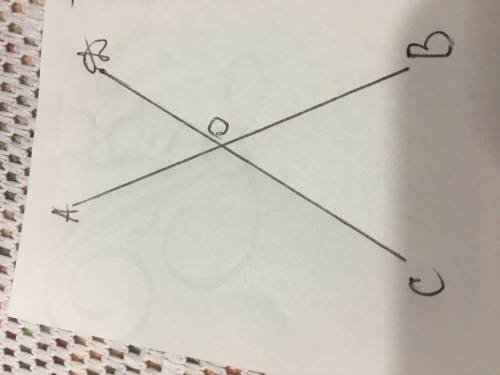
При пересечении двух прямых образовались 4 угла,и эти четыре угла равны 360 градусов,получилось две пары вертикальных углов
<АОD=<COB,как вертикальные
<АОС=<DOB,как вертикальные
<АОD=X
<COB=X
<AOC=2X
<DOB=2X
X+X+2X+2X=360 градусов
6Х=360
Х=360:6
Х=60
<АОD=<COB=60 градусов
<АОС=<DOB=60•2=120 градусов
Объяснение:
Вопрос стоит так-сумма двух углов равна градусной мере третьего угла
Два вертикальных угла по 60 градусов,а один угол из другой пары вертикальных углов равен 120 градусов
60+60=120 градусов,что и следовало доказать
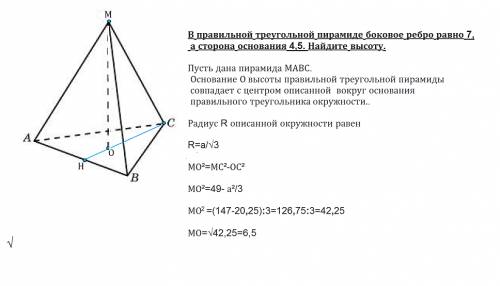
Вписанный угол равен половине дуги, на которую опирается
х - одна часть
2х+3х+4х=360
х=40
40*2=80; 40*3=120; 40*4=160
Значит, окружность разбита на дуги 80°, 120° и 160°.
Угла треугольника соответственно равны 40°, 60° и 80°.