Ну, раз такие задачи тут мелькают, придется сказать пару ласковых слов.
1. Уж не ждите, что в подобных задачах я стану "разжевывать" решение.
2. Всю теорию, которую я буду использовать, я буду считать априори известной автору такой задачи. Поэтому не ждите от меня краткого изложения учебника геометрии.
3. Все "спорные" моменты выносите на обсуждение, только если другого выхода нет. Попытки задать вопрос вроде "а почему 2х2?" будут жестоко высмеяны и оставлены без ответа.
4. Жаловаться не надо - сами виноваты, надо было разобраться.
"Решение", которого нет...
Пусть стороны, имеющие с биссектрисой l общую вершину - a и c, а сторона, которую нужно найти - b.
Сразу видно, что
b/(a + c) = 2/3;
Поэтому сторона b делится биссектрисой на два отрезка (2/3)*а и (2/3)*с;
Если предположить, что треугольник равнобедренный, то найти стороны не составляет труда.
с = а = 6*корень(5); b = (2/3)*(а + c) = 8*корень(5);
Теперь проведем через точку О (пересечение биссектрис) и концы основания этого равнобедренного треугольника окружность.
Легко видеть, что это - окружность Апполония для биссектрисы l при отношении 2/3; (: обожаю этот момент :
Параметры этой окружности таковы - радиус R = 12, центр расположен на прямой, содержащей биссектрису, на расстоянии 8 от пересечения со стороной b, за ней, конечно, то есть на расстоянии 12 от точки О и 18 от "начала" биссектрисы.
Поэтому в задаче нет однозначного решения, а полученный результат для равнобедренного треугольника b = 8*корень(5) является минимальным решением задачи. Максимальное решение получается при угле при вершине, равном нулю, при этом b равно диаметру окружности Апполония, то есть 24.
Любой треугольник, концы строны b которого лежат на построенной окружности, а хорда b проходит через конец биссектрисы, соответствует условию задачи.
Это всё :
Cosα = 2/9, α ≈ 77,1°
Объяснение:
В правильном тетраэдре все ребра равны, а грани - правильные треугольники.
Центры граней - точки пересечения медиан (высот, биссектрис).
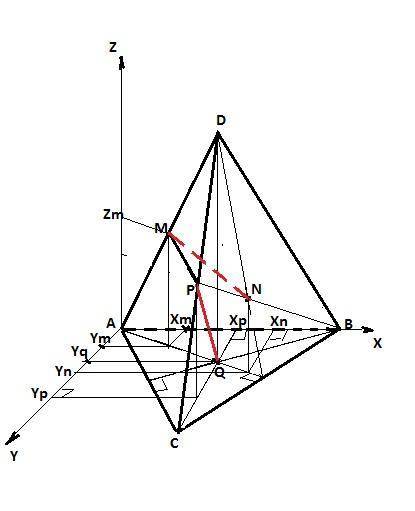
Привяжем систему прямоугольных координат к вершине А и найдем координаты нужных нам для решения точек учитывая, что высота правильного треугольника равна h=(√3/2)*а, высота правильного тетраэдра равна H=√(2/3)*а, медианы в точке пересечения делятся в отношении 2/3, считая от вершины, <BAC=60° => <BAH=30°,
<YpAH = 60°. Тогда
А(0;0;0).
Q(a/2;(√3/6)а;0) - так как Хq = Xp = a/2, Yq = (2/3)*h*Cos60.
М(a/4;√3a/12;(√(2/3))*а/2) - так как Xm = Xq/2, Ym = Yq/2, Zm =H/2 - из подобия треугольников).
P(a/2;(√3/3)*а;(√(2/3))*а/2) - так как Xp=Xq, Yp=(2/3)*h, Zp=Zm.
N(2a/3 ;(2√3/9)a;√(2/3))*а/3)- так как Xn=Xq+(2/3)*(1/3)*h*Cos30, Yn=Yq+(2/3)*(1/3)*h*Cos60, Zn=(1/3)*H.
Примем а=1. Тогда
Вектор PQ{0;-√3/6; -(√(2/3)/2}. |PQ| = √(0+3/36+1/6) = 1/4.
Вектор MN{5/12;5√3/36; -(√(2/3)/6}.
|MN| = √(25/144+75/1296+1/54) = 324/1296 = 1/4.
Cosα = |(Xpq*Xmn+Ypq*Ymn+Zpq*Zmn)/(|PQ|*|MN|) или
Cosα = |(0-5/72+1/18)/((1/4)*1/4)| = |(-1/72)/(1/16)| = 2/9.
α ≈ 77,1°
Вариант 1
А1-2
Посмотрите есть ли опечатка в А2