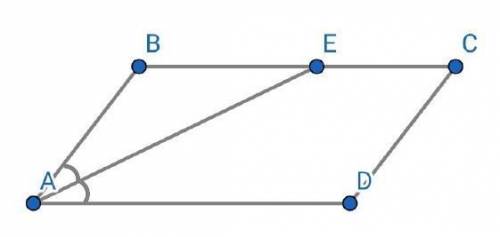
Четырёхугольник ABCD — параллелограмм.
Отрезок АЕ — биссектриса ∠А.
Е ∈ ВС.
ВЕ = 3*ЕС.
ВС = 12 [см].
Найти :Р(ABCD) = ?
Решение :Пусть ЕС = х, тогда, по условию задачи, ВЕ = 3х.
ВС = ВЕ + ЕС
12 [см] = 3х + х
4х = 12 [см]
х = 3 [см].
ВЕ = 3х = 3*3 [см] = 9 [см].
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.Следовательно, ∆АВЕ — равнобедренный (причём ВЕ = АВ = 9 [см]).
Периметр параллелограмма равен удвоенной сумме его смежных сторон.Следовательно, Р(ABCD) = 2*(AB + BC) = 2*(9 [см] + 12 [см) = 2*21 [см] = 42 [см].
ответ :42 [см].
Объяснение:
1) знайдемо більшу сторону основи : 5²+12²=25+144=169 √=13 см , знайдемо площу основи , 1/2*5*12=30 см² , основ дві тому 2*30=60 см², шукаємо площі бічних сторін: 12*10+5*10+13*10=120+50+130=300 см²
тепер все разом: 300+60=360 см²
3) розрізали ціліндр по осі, в перерізі маємо квадрат, сторона якого є діаметром, площа квадрата за умовою є36 см², тому сторона квадрата(діаметр) буде 6 см. Тепер шукаємо площі основ і бокову поверхню циліндра. В основі циліндра є площа круга , S круг.=πД²/4=π6²/4=18πсм² основ двы , тому площа основ = 36π см², бокова поверхня циляндра є прямокутник , основа якого є довжина кола * на висоту . С=π*Д=6π а так як висота теж дорівнює діаметру, маємо бокову поверхню 36π Площа повної поверхні буде:36π+18π=54 π