ответ: 8 см²
Объяснение:
КАК решают такие задачи.
Часто подобные задачи решаются вычитания ( или сложения ) площади фигур, образованных клетками. Чертят прямоугольник, который описывает данную фигуру. Вычисляют его площадь, затем площадь "лишних"фигур ( обычно это треугольники) и вычитают. Остается искомая площадь . Или делят данную фигуру на части, у которых удобно найти площадь, и затем складывают.
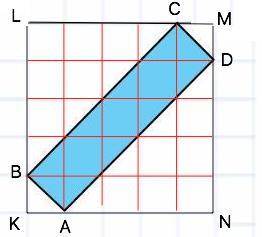
Обозначим прямоугольник АВСD, опишем около него прямоугольник KLMN. (см. вложение).
S(KLMN)=KL•LM=5•5=25 см²
∆BLC=∆AND по равным катетам.
Их общая площадь Ѕ₁=4•4=16 см²
∆BKA=∆CMD по равным катетам. Их общая площадь
Ѕ₂=1•1=1 см²⇒
Ѕ (ABCD)=S (KLMN)- 16-1=8 см²
----------
Другой
Из ∆ (BLC) по т.Пифагора найдем длину ВС=√(4²+4²)=4√2 см.
Из ∆ (ВКС) по т.Пифагора найдем ширину АВ=√(1²+1²)=√2 см
Площадь прямоугольника равна произведению его длины на ширину:
S(ABCD)=ВС•АВ=4√2•√2=8 см²
1. Каждая сторона треугольника составлена из 2 таких отрезков. Поэтому их длины будут 3+4 = 7, 3+5 = 8 и 4+5 = 9... это обычный остроугольный треугольник без особых примет. Уж точно не прямоугольный.
2. Дуга АСВ равна 150 градусам, а дуга АМВ - 210 градусов. Угол АМВ опирается на дугу АСВ, то есть равен 150/2 = 75 градусов, угол АВМ = 90 градусов - АМ диаметр, угол АСВ = 210/2 = 105 градусов (независимо от положения точки С).
3. пусть CE = 3*x; ED = 4*x; CD = 7*x;
(3*x)*(4*x) = 3*36; x = 3;
CD = 21; наименьшее значение радиуса - если АВ еще "влезает" в окружность, то есть 39/2 = 19,5
4. Половина основания 6, площадь 48, периметр 32, r = 2*S/P = 3;
R = 10*10*12/(4*S) = 25/4;
4 пункт подробнее с чертежом и другим решением
Изображение сечения на прикрепленных фото)