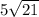c= 27.572
A=65.87
B=39.28
Объяснение:
по теореме косинусов:
с^2=a^2+b^2-2ab*cos75
c=корень(a^2+b^2-2ab*cos75) = корень(26^2+18^2-2*26*18*0.25)=
=корень(676+324-242.24)=корень(757.76)=27,572
по теореме синусов
a/sin.угла A = b/sin.угла B = c/sin.угла C
=> c/sin.угла C= 27.527/sin75 = 27.527/0.966=28.495
A=arccos(b^2+c^2-a^2/2bc)= arccos(18^2+27.572^2-26^2/2*18*27.572)=
= arccos(324+757.76-676/992.592)=arccos(0.4087883037542)=65.87
B = arccos(a^2+c^2-b^2/2ac)= arccos(676+757.76-324/1433.744)=
=arccos(0.774029)=39.28
Объяснение:
Задача № 1.
Дано: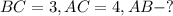 
Решение: Так как ABC - прямоугольный треугольник, то AB можно найти по теореме Пифагора:
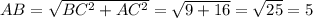
ответ: 5.
Задача № 2.
Дано: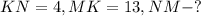 
Решение: Так как NMK - прямоугольный треугольник, то NK можно найти по теореме Пифагора:
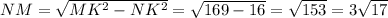
ответ: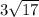 
Задача № 3.
Дано: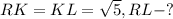 
Решение: так как RKL - прямоугольный треугольник, то RL найдем через теорему Пифагора:
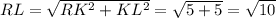
ответ: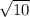 
Задача № 4.
Дано: ∠M = 30°,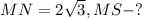 
Решение: MNS - прямоугольный треугольник:
1. Так как катет NS лежит напротив 30 градусов, то он равен половине гипотенузы:
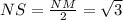
2. Найдем катет MS через теорему Пифагора:
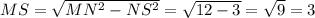
ответ: 3
Задача № 5.
Дано: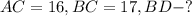 
Решение: Рассмотрим треугольник BDC - прямоугольный:
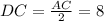- так как высота делит основание пополам в равнобедренном треугольнике
BD найдем по теореме Пифагора:
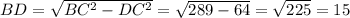
ответ: 15
Задача № 6.
Дано: ΔRMN - правильный,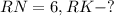 
Решение: Рассмотрим ΔRKN - прямоугольный:
1. Высота делит основание пополам в правильном треугольнике:
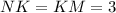
2. Найдем высоту по теореме Пифагора:
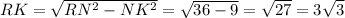
ответ: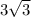 
Задача № 7.
Дано: ΔMPR - правильный,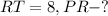 
Решение: Рассмотрим ΔPTR - прямоугольный:
1. Высота делит основание пополам, тогда:
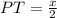
2. Найдем PR через теорему Пифагора:
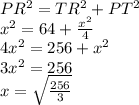
Отрицательный корень нам не подходит, так как длина отрезка не может быть отрицательной.
ответ: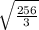 
Задание № 8.
Дано: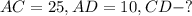 
Решение: Рассмотрим ΔACD - прямоугольный:
Найдем CD по теореме Пифагора:
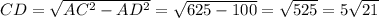
ответ: 
